Ajuste e avaliação de modelos de crescimento em altura dominante
Na mensuração florestal a utilização de modelos de regressão para representação de comportamentos biológicos é uma tarefa comum. Para dada variável a ser modelada o teste de diferentes modelos é necessário para aplicação daquele que melhor representa o comportamento sob análise. O método tradicionalmente aplicado para classificação de sítios florestais exige o emprego de modelos de crescimento em altura dominante, e o ajuste e análise destes será objeto desta postagem.
Começaremos importando uma base de dados de povoamentos de Pinus taeda.
# Importar dados
library(readxl)
dados <- read_excel("dados_processados.xlsx")
dados## # A tibble: 813 × 9
## PARCELA ESPÉCIE IDADE DAP ALTURA N HDOM G VOLTOT
## <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 PINUS TAEDA 19.8 24.1 23.6 927. 25.5 44.5 509.
## 2 2 PINUS TAEDA 19.8 25.1 24.0 748. 25.6 38.1 436.
## 3 3 PINUS TAEDA 24.2 28.0 26.6 700 26.3 44.6 563.
## 4 4 PINUS TAEDA 24.2 30.3 25.9 600. 29.9 44.9 551.
## 5 5 PINUS TAEDA 24.2 32.0 27.9 600 31.3 49.4 655.
## 6 6 PINUS TAEDA 24.2 30.7 27.4 650 29.5 50.1 657.
## 7 7 PINUS TAEDA 24.2 30.8 25.3 583. 27.2 44.5 532.
## 8 8 PINUS TAEDA 24.2 30.0 26.2 640. 30.3 46.7 579.
## 9 9 PINUS TAEDA 24.2 30.4 26.4 633. 31.1 47.2 594.
## 10 10 PINUS TAEDA 24.2 28.2 26.4 620. 29.2 40.1 507.
## # ℹ 803 more rows#Visualizar a relação Idade x Altura dominante
plot(HDOM~IDADE, data = dados,
xlim = c(0,30), ylim = c(0,35),
xlab = 'Idade (anos)', ylab = 'Hdom (m)')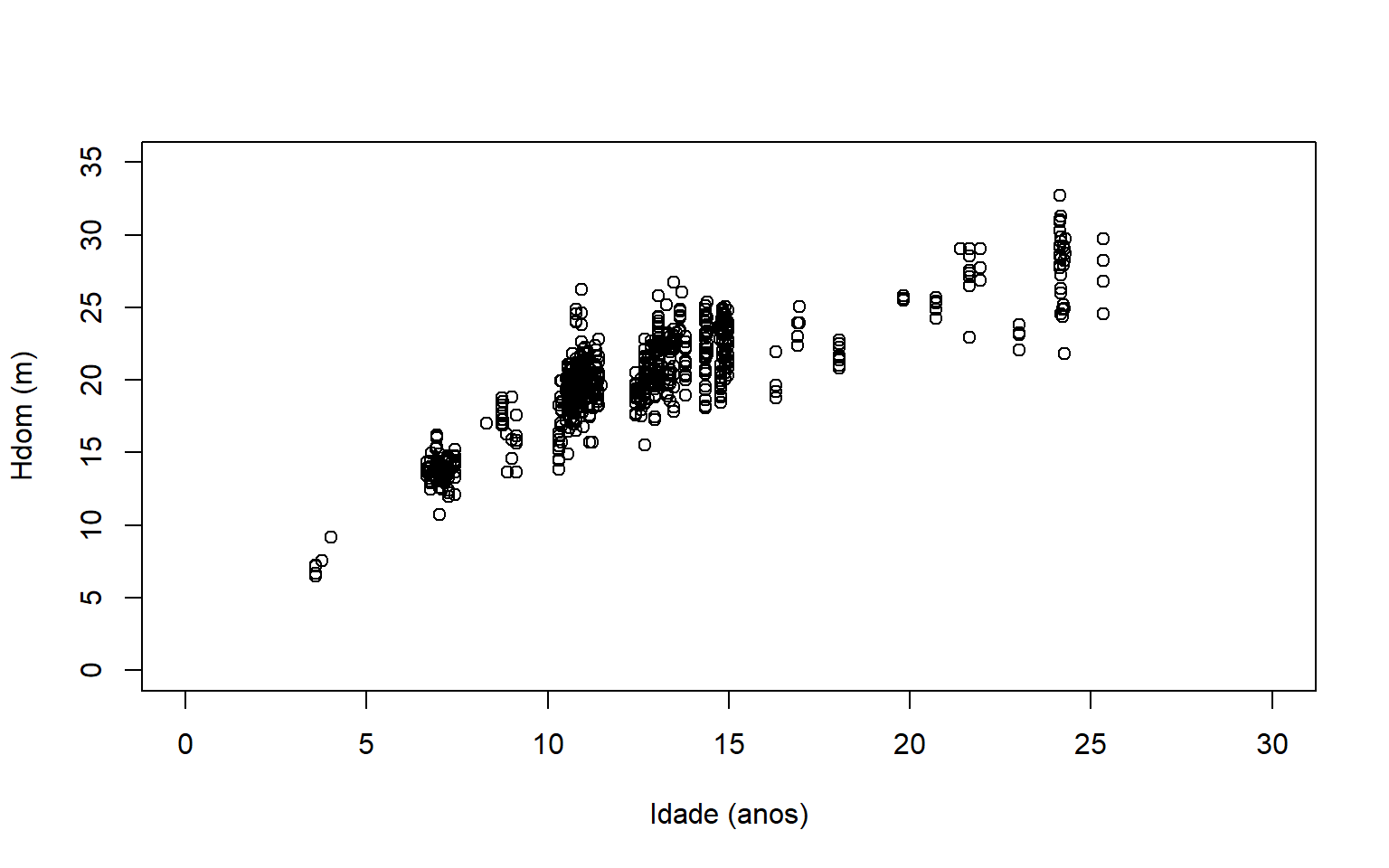
Nosso trabalho agora será ajustar diversos modelos e avaliar qual deles melhor representa os dados em questão. Testaremos os seguintes modelos.
| Modelo | Expressão matemática |
|---|---|
| Chapman-Richards | |
| Lundvist-Korf | |
| Bailey-3 parâmetros | |
| Clutter-Jones |
Para o ajuste dos modelos utilizaremos a função nlsLM do pacote minpack.lm. A diferença entre esta e a função nls é o algoritmo de busca dos parâmetros. A função nlsLM utiliza o algoritmo Levenberg-Marquardt que é mais eficiente que o Gauss-Newton utilizado pela nls, especialmente quando não temos referências iniciais para declarar ao argumento start, e/ou quando buscamos ajustar modelos com maior quantidade de parâmetros.
# Ajustar modelos de crescimento em altura dominante
library(minpack.lm)
chapman_richards <- nlsLM(HDOM ~ b0*(1-exp(-b1*IDADE))^b2,
start=list(b0=30,b1=0.5,b2=1), control = nls.control(maxiter = 1024),
data = dados)
lundqvist_korf <- nlsLM(HDOM ~ b0*exp(-b1*(1/(IDADE^b2))),
start = list(b0=40,b1=5,b2=0.5), control = nls.control(maxiter = 1024),
data = dados)
bailey_3p <- nlsLM(HDOM ~ b0*(1-exp(-b1*IDADE^b2)),
start = list(b0=24,b1=0.05, b2=1.5), control = nls.control(maxiter = 1024),
data = dados)
clutter_jones = nlsLM(HDOM ~ b0*(1+b1*IDADE^b2)^b3,
start=list(b0=25,b1=-0.2, b2=-0.1, b3=20), control = nls.control(maxiter = 1024),
data = dados)
# Armazenar modelos em uma lista
modelos <- mget(c('chapman_richards', 'lundqvist_korf', 'bailey_3p', 'clutter_jones'),
envir = globalenv())A vantagem de armazenar modelos em listas é que podemos analisá-los por meio de scripts mais compactos. Por exemplo, com uma única linha de código podemos acessar os coeficientes de todos os modelos empregando a função lapply.
lapply(modelos, coefficients)## $chapman_richards
## b0 b1 b2
## 29.4572596 0.1096941 1.1937825
##
## $lundqvist_korf
## b0 b1 b2
## 39.211720 5.203893 0.832053
##
## $bailey_3p
## b0 b1 b2
## 29.40328604 0.07718152 1.09415279
##
## $clutter_jones
## b0 b1 b2 b3
## 40.2647981 -0.4400840 -0.7712678 10.2314371A seguir vamos gerar os gráficos da curva de ajuste, de dispersão e de distribuição de resíduos em classes de erro. Em vez de criarmos todos os gráficos um a um, apresentaremos a lista de modelos a uma função que gera os três gráficos para cada elemento da lista.
library(ggplot2)
library(egg)
library(tibble)
library(dplyr)
library(purrr)
library(stringr)
# Idade máxima de predição
idmax = 25
# Função para gerar análise gráfica de modelos
graficos = syms(names(modelos)) %>% set_names() %>%
imap(function(modelo, nome_modelo) {
# Obter o modelo
modelo = eval(modelo)
# Formatar nome do modelo
nome_modelo = str_to_title(gsub("_", "-", nome_modelo))
# Criar os dados para predição
dados_ajuste = eval(modelo$data)
dados_predicao = tibble(IDADE = seq(0, idmax, 0.1))
dados_predicao$HDOM = predict(modelo, newdata=dados_predicao)
# Listar gráficos
list(curva_ajuste = ggplot(dados_predicao, aes(IDADE, HDOM)) +
geom_line() +
geom_point(data=dados_ajuste, alpha=0.2) +
scale_x_continuous(expand=expand_scale(mult=c(0,0.01)), breaks = seq(0,idmax,2)) +
scale_y_continuous(expand=c(0,0)) +
labs(x='Idade (anos)', y='Hdom (m)',
title = paste0(nome_modelo,' - Syx = ', round(summary(modelo)$sigma, 2)))+
theme_light(),
dispersao_residuos = ggplot(tibble(x=dados_ajuste$IDADE, y=residuals(modelo)/mean(x)*100)) +
geom_point(alpha=0.2, aes(x, y)) +
geom_hline(yintercept=0) +
scale_x_continuous(expand=expand_scale(mult=c(0,0.01))) +
scale_y_continuous(expand=c(0,0), limits = c(-50,50)) +
labs(x='Idade (anos)', y='Desvio (%)')+
geom_line(stat = 'smooth', method = 'loess', aes(x, y), color = 'red', alpha = .8,
size = 1, linetype ="dashed",)+
theme_light(),
distribuicao_residuos = ggplot(tibble(x=residuals(modelo)/mean(dados_ajuste$HDOM)*100)) +
geom_histogram(aes(x, y=..count../nrow(dados_ajuste)*100), breaks=seq(-27.5,27.5,by=5),
colour='black') +
labs(x='Classe', y='Frequência (%)') +
scale_y_continuous(limits=c(0,30))+
theme_light()
)
})
# Plotar todos os gráficos em uma única imagem
map(graficos, ~ggarrange(plots=.x, ncol=3, draw=FALSE)) %>%
grid.arrange(grobs=., ncol=1)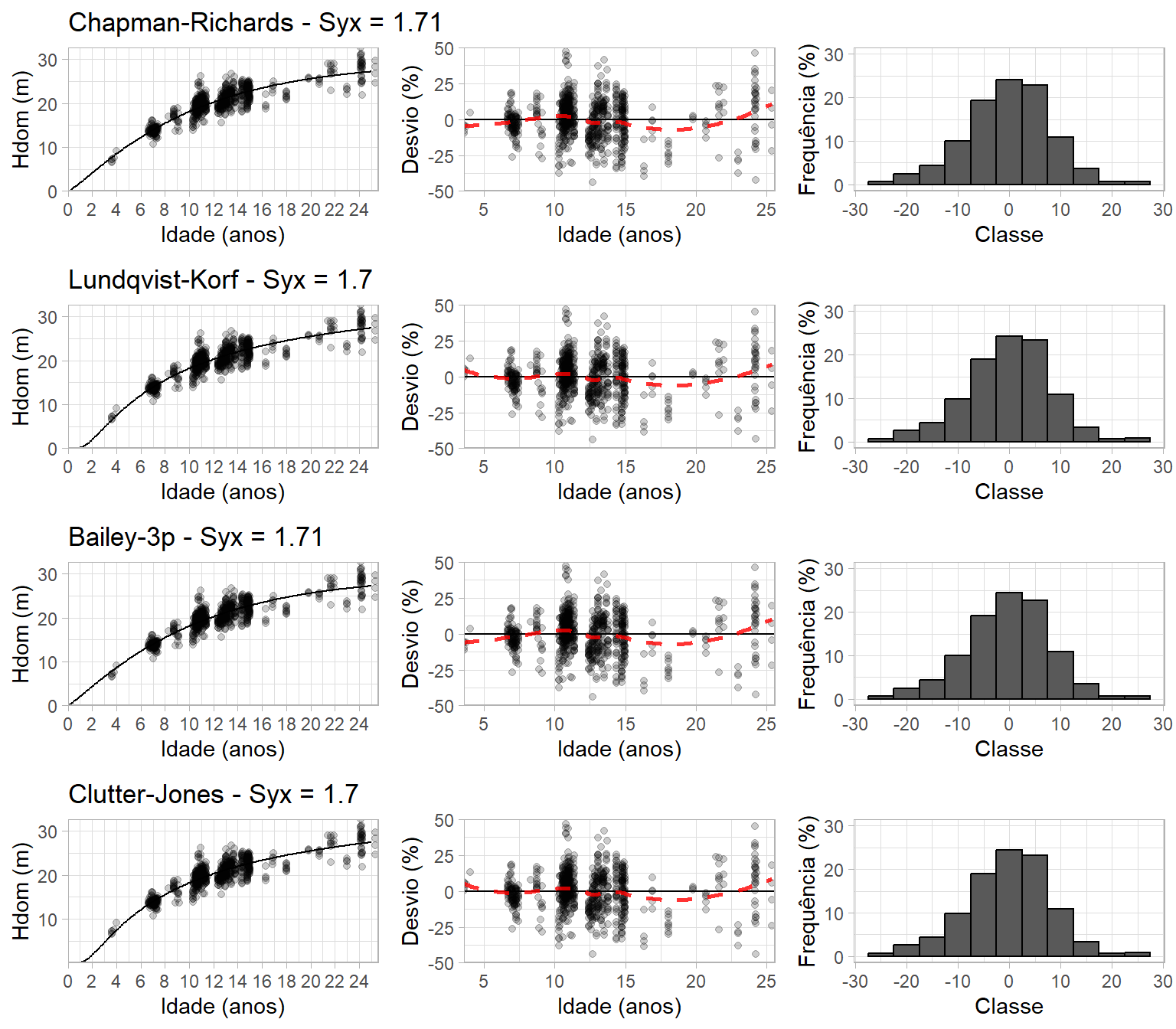 Os quatro modelos tiveram desempenho bastante similar para os gráficos de resíduos e para o erro padrão das estimativas. No entanto, há uma diferença considerável nas assíntotas (coeficiente b0) e nas predições de altura dominante para idades inferiores a 3 anos. Os modelos de Lundqvist-Korf e Clutter-Jones sugerem que no futuro as árvores dominantes alcançarão em média os 40 metros de altura, enquanto os modelos de Chapman-Richards e Bailey-3p indicam que a assíntota se dá em torno de 30 metros. Esta é uma questão pouco relevante se considerarmos que neste caso os povoamentos serão submetidos a corte raso entre os 14 e os 16 anos, e que nesta faixa de idade temos uma quantidade suficiente de amostras.
Os quatro modelos tiveram desempenho bastante similar para os gráficos de resíduos e para o erro padrão das estimativas. No entanto, há uma diferença considerável nas assíntotas (coeficiente b0) e nas predições de altura dominante para idades inferiores a 3 anos. Os modelos de Lundqvist-Korf e Clutter-Jones sugerem que no futuro as árvores dominantes alcançarão em média os 40 metros de altura, enquanto os modelos de Chapman-Richards e Bailey-3p indicam que a assíntota se dá em torno de 30 metros. Esta é uma questão pouco relevante se considerarmos que neste caso os povoamentos serão submetidos a corte raso entre os 14 e os 16 anos, e que nesta faixa de idade temos uma quantidade suficiente de amostras.
Por outro lado, as curvas geradas por esses pares de modelos também apresentam comportamento divergente para idades inferiores a 4 anos, em que não há observações. Neste caso os modelos de Lundqvist-Korf e Clutter-Jones sugerem que povoamentos com 1 ano de idade possuem altura dominante igual a zero, o que é bastante equivocado do ponto de vista biológico. O problema na utilização destes modelos se daria se, por alguma razão, houvesse a necessidade de predizer o sítio em povoamentos cuja idade no momento do inventário é inferior a 3 anos. Em todos os casos não temos observações para representar o crescimento em idades inferiores a 4 anos, mas o bom senso, a experiência e a lógica são suficientes para nos garantir que povoamentos com um ano de idade já possuem algum crescimento em altura.
Então, para concluir, já que os modelos apresentaram grande similiaridade entre si para as análises de resíduos, eu escolheria o modelo de Chapman-Richards ou Bailey-3p para representar o crescimento em altura dominante deste povoamento, tomando por base o comportamento biológico esperado.