Cálculo de índices ecológicos

As análises fitossociológicas contemplam a utilização de índices ecológicos que exprimem a riqueza e a diversidade de comunidades vegetais, permitindo a comparação e o monitoramento dos recursos vegetais, além de fornecer subsídios ao seu manejo.
Nesse post calcularemos praticaremos o cálculo dos seguintes índices:

Índice	Fórmula	Descrição
Índice de Margalef	$D_{Mg}=\frac{S-1}{ln(N)}$	Expressa riqueza de espécies
Índice de Shannon	$H^{\prime }=-\sum \frac{n_i}{N}ln(\frac{n_i}{N})$	Expressa a heterogeneidade da composição florística ou o grau de incerteza em relação à espécie de um indivíduo amostrado ao acaso
Índice de Simpson	$D=-\sum {\left(\frac{n_i}{N}\right)}^2$	Expressa a dominância de espécies e a probabilidade de dois indivíduos amostrados ao acaso pertencerem à mesma espécie
Índice de Pielou	$J^{\prime }=\frac{H^{\prime }}{ln(S)}$	Exprime a equitabilidade, ou seja, o padrão de distribuição dos indivíduos entre as espécies.

Em que: $S$ = número de espécies amostradas; $N$ = quantidade de indivíduos amostrados; $n_i$ = quantidade de indivíduos amostradados da espécie $i$;$ln$ = logaritmo natural.
Vamos às análises. Iniciaremos importando a mesma base de dados utilizada no post em que analisamos a estrutura horizontal e e também no post em que construímos curvas de acumulação de espécies e de rarefação. A seguir calcularemos todos os índices ecológicos acima apresentados, com auxílio do pacote vegan.
Obs: Para baixar os dados utilizados nesse exemplo, clique aqui.

# Importar dados
dados <- readxl::read_excel("dados_fitossociologia.xlsx")
# Visualizar dados
dados

## # A tibble: 541 × 6
##    Parcela Arvore   DAP Altura Familia         Especie              
##      <dbl>  <dbl> <dbl>  <dbl> <chr>           <chr>                
##  1       1      1 13.5     5   Dilleniaceae    Curatella americana  
##  2       1      2  5.57    3.5 Annonaceae      Annona coriacea      
##  3       1      3  5.09    4   Lauraceae       Ocotea minarum       
##  4       1      4  5.25    4   Lauraceae       Ocotea minarum       
##  5       1      5 11.8     4   Ebenaceae       Diospyros hispida    
##  6       1      6  7.96    5.5 Fabaceae        Copaifera langsdorfii
##  7       1      7  8.91    4.5 Sapindaceae     Matayba elaegnoides  
##  8       1      8  5.89    3.5 Ebenaceae       Diospyros hispida    
##  9       1      9  8.75    4.5 Ebenaceae       Diospyros hispida    
## 10       1     10  4.77    2.5 Melastomataceae Miconia sp1          
## # ℹ 531 more rows

# Carregar pacotes necessários
library(vegan)
library(dplyr)
# Gerar matriz de frequência das espécies
matriz_freq <- xtabs(~Parcela+Especie, dados)
# Pacotes para geração da tabela em HTML
library(knitr)
library(kableExtra) 
library(dplyr)
# Visualizar a matriz de frequência (cada linha é uma unidade amostral)
kable(matriz_freq[1:6,])%>%
  kable_styling(fixed_thead = T)

Alibertia edulis	Anadenanthera falcata	Andira cuiabensis	Annona coriacea	Annona crassiflora	Bauhinia rufa	Bauhinia ungulata	Buchenavia tomentosa	Byrsonima basiloba	Byrsonima coccolobifolia	Byrsonima pachyphylla	Byrsonima verbascifolia	Calliandra sp1	Campomanesia adamantium	Caryocar brasiliense	Casearia sylvestris	Connarus suberosus	Copaifera langsdorfii	Couepia grandiflora	Curatella americana	Dimorphandra mollis	Diospyros hispida	Dipteryx alata	Eriotheca gracilipes	Erythroxylum suberosum	Eugenia aurata	Eugenia punicifolia	Handroanthus albus	Himenaea courbaril	Indeterminada 1	Indeterminada 2	Kielmeyera coriacea	Lafoensia pacari	Leptolobium elegans	Machaerium acutifoium	Magonia pubescens	Matayba elaegnoides	Miconia sp1	Myrcia sp1	Ocotea minarum	Ouratea hexasperma	Ouratea spectabilis	Pouteria ramiflora	Pouteria torta	Psidium laruotteanum	Qualea grandiflora	Qualea parviflora	Rhamnidium elaeocarpum	Roupala montana	Schefflera macrocarpa	Syagrus flexuosa	Tabebuia aurea	Tachigali aurea	Tapirira guianensis	Terminalia argentea	Vatairea macrocarpa	Vochysia cinnamomea	Xylopia aromatica
0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	4	0	3	0	0	0	2	0	0	0	0	0	0	0	0	0	0	0	0	0	0
2	0	0	1	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	2	0	0	0	4	0	1	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	6	0	2	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	4	1	0	0	0	0	1	0	1	0	0	0	0	0	0	0	0	1	0	0	0
0	0	2	1	1	0	0	0	0	0	0	0	0	0	0	0	1	0	0	4	0	3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	4	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0	1
0	0	1	2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	3	0	0	0	0	0	0	0	1	0	1	0	0	0	4	0	0	0	0	0	0	0	1	0	0	0	0	0	1
0	0	0	0	0	0	0	0	1	0	0	0	0	1	0	0	0	1	0	3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	7	0	1	0	0	0	2	0	0	0	0	0	0	0	0	1	0	0	0	0	0

# Número de indivíduos por parcela
n_ind_parc <- rowSums(matriz_freq)
# Número total de indivíduos amostrados
n_ind_tot <- sum(n_ind_parc)
# Número de espécies
n_sp_parc <- specnumber(matriz_freq)
# Número de espécies total
n_sp_tot <- specnumber(colSums(matriz_freq))
# Índice de Margalef para cada parcela
margalef_parc <- (n_sp_parc-1)/n_ind_parc
# Índice de Margalef para toda a comunidade
margalef_tot <- (n_sp_tot-1)/n_ind_tot
# Índice de Shannon para cada parcela
simpson_parc <- diversity(matriz_freq, index = 'simpson')
# Índice de Shannon para toda a comunidade
simpson_tot <- diversity(colSums(matriz_freq), index = 'simpson')
# Índice de Shannon para cada parcela
shannon_parc <- diversity(matriz_freq, index = 'shannon')
# Índice de Shannon para toda a comunidade
shannon_tot <- diversity(colSums(matriz_freq), index = 'shannon')
# Equabilidade de Pielou para cada parcela
pielou_parc <- shannon_parc/log(n_sp_parc)
# Equabilidade de Pielou para toda comunidade
pielou_tot <- shannon_tot/log(n_sp_tot)

# Gera tabela de resultados
tabela_indices <- data.frame(Parcela = names(margalef_parc),
                             Margalef = round(margalef_parc,2),
                             Simpson = round(simpson_parc,2),
                             Shannon = round(shannon_parc,2),
                             Pielou = round(pielou_parc,2))
tabela_indices <- bind_rows(tabela_indices,data.frame(Parcela = 'Total',
                                                  Margalef = round(margalef_tot,2),
                                                  Simpson = round(simpson_tot,2),
                                                  Shannon = round(shannon_tot,2),
                                                  Pielou = round(pielou_tot,2)))
knitr::kable(tabela_indices, row.names = FALSE)%>%
  kableExtra::kable_styling(full_width = T, position = "center",fixed_thead = T)

Parcela	Margalef	Simpson	Shannon	Pielou
1	0.44	0.84	1.93	0.93
2	0.47	0.84	1.93	0.93
3	0.47	0.83	2.01	0.87
4	0.47	0.86	2.11	0.92
5	0.53	0.84	2.03	0.92
6	0.44	0.79	1.87	0.85
7	0.33	0.68	1.36	0.84
8	0.57	0.85	2.04	0.93
9	0.78	0.86	2.04	0.98
10	0.79	0.91	2.44	0.98
11	0.48	0.88	2.38	0.90
12	0.46	0.83	2.19	0.85
13	0.53	0.88	2.23	0.93
14	0.40	0.86	2.06	0.94
15	0.53	0.88	2.20	0.96
16	0.63	0.91	2.48	0.97
17	0.42	0.76	1.78	0.81
18	0.58	0.92	2.66	0.96
19	0.47	0.74	1.83	0.80
20	0.50	0.81	2.27	0.82
21	0.45	0.87	2.21	0.92
22	0.50	0.75	1.49	0.93
23	0.56	0.81	1.74	0.97
24	0.43	0.87	2.16	0.94
25	0.50	0.80	1.70	0.95
26	0.56	0.84	2.10	0.91
27	0.52	0.90	2.40	0.94
28	0.30	0.79	1.98	0.80
29	0.50	0.89	2.35	0.95
Total	0.11	0.95	3.51	0.86

A tabela acima apesenta todos os parãmetros ecológicos calculados a nível de parcela e também para toda a comunidade.
Outro indicador ecológico comumente utilizado em estudos fitossociológicos é o Índice de Jaccard, que expressa a similaridade de espécies entre os locais amostrados, rendo a seguinte expressão matemática:

$J=\frac{C}{A+B+C}$

Em que: $A$ = número de espécies presentes na parcela A e ausentes na parcela B; $B$ = número de espécies presentes na parcela B e ausentes na parcela A; $C$ número de espécies presentes nas parcelas A e B.

# Índice de similaridade de Jaccard
indice_jaccard <- betadiver(matriz_freq,'j')

Por fim, podemos analisar visualmente as relações de similaridade entre as parcelas ou adrupamento dessas por meio de um dendrograma. No gráfico abaixo podemos observar que as parcelas que, individualmente, apresentaram maior similaridade entre si foram 20 e 29.

# Gerar dendrograma
dendrograma <- hclust(indice_jaccard)
par(mfrow=c(1,1),mar=c(1,4,3,1))
plot(dendrograma, hang=1,
     main = 'Dendrograma de similaridade',
     ylab='Similaridade')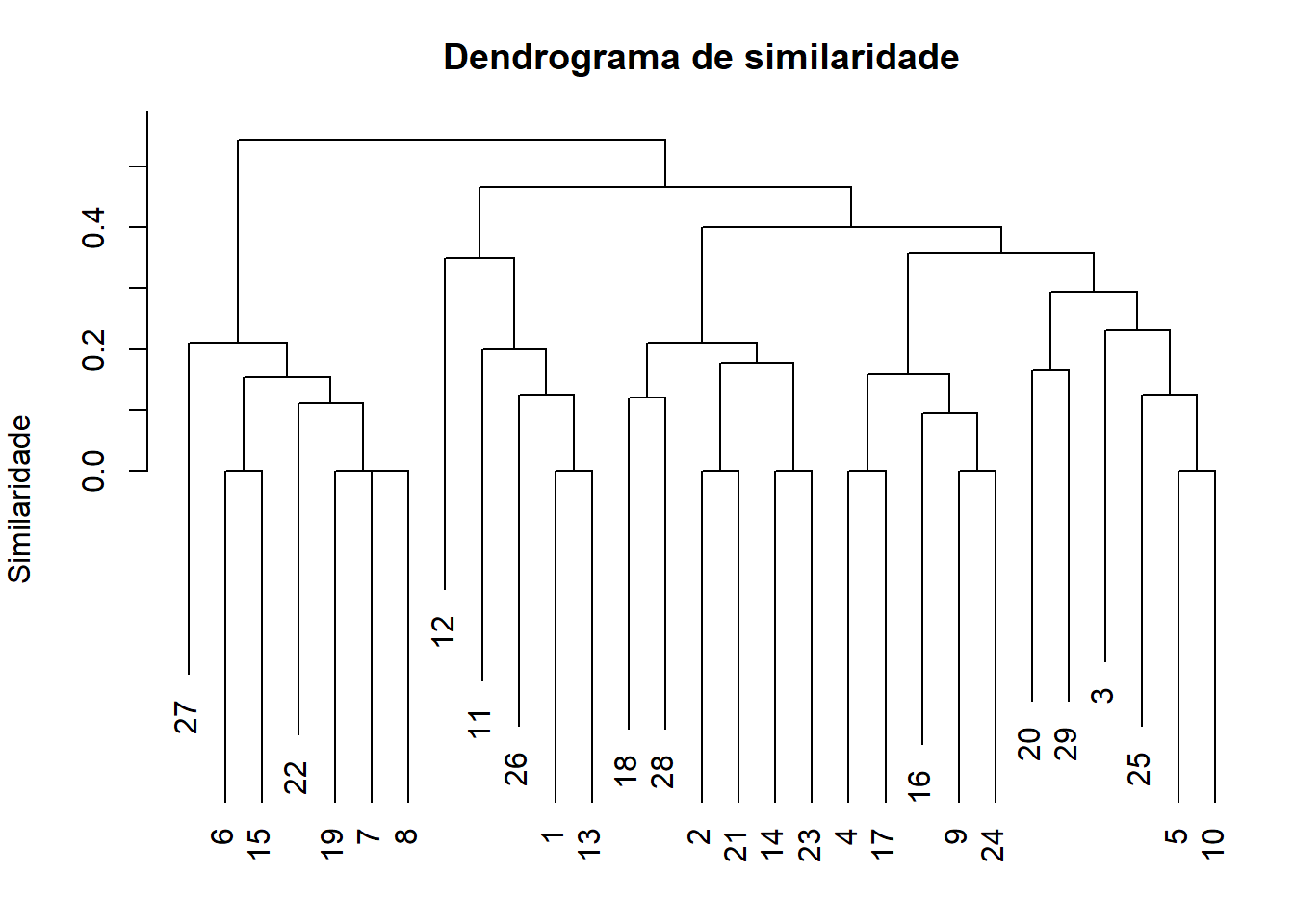

O dendrograma de similaridade é especialmente interessante para avaliar a a semelhança entre comunidades, embora possa também ser aplicado para comparar unidades amostrais em uma mesma comunidade. No presente exemplo, as unidades amostrais possuem área de 100 m², resultando em informações bastante limitadas a nível de parcela. Para este tipo de avaliação, unidades amostrais de maiores dimensões são mais adequadas pois reduzem a variação entre parcelas, permitindo uma avaliação mais abrangente.