Curvas de rarefação e acumulação de espécies
A riqueza de espécies é o mais simples e usual descritor da diversidade biológica, mas há uma grande dificuldade em determinar o quanto se deve amostrar para estimar com confiabilidade o número de espécies esperado em uma comunidade vegetal.
Uma ferramenta bastante utilizada para esta finalidade é a curva de acumulação de espécies, também conhecida como curva do coletor, que relaciona o número de novas espécies encontradas a medida em que se aumenta o número de amostras ou a área amostral.
Um problema encontrado na construção da curva do coletor é a arbitrariedade na ordem de entrada das unidades amostrais, já que cada possível ordenação pode gerar uma curva diferente, invalidando qualquer interpretação com base em sua forma.
Para contornar esse problema devemos utilizar uma curva suavizada, que consiste em uma curva média obtida a partir de um grande número de curvas geradas por procedimentos de aleatorização das unidades amostrais.
A função specaccum, implementada no pacote vegan do R, é capaz de gerar uma curva de acumulação de espécies suavizada do modo descrito acima, conforme o procedimento a seguir.
Obs: Para baixar os dados utilizados nesse exemplo, clique aqui.
# Importar dados
dados <- readxl::read_excel("dados_fitossociologia.xlsx")
# Visualizar dados
dados## # A tibble: 541 × 6
## Parcela Arvore DAP Altura Família Espécie
## <dbl> <dbl> <dbl> <dbl> <chr> <chr>
## 1 1 1 13.5 5 Dilleniaceae Curatella americana
## 2 1 2 5.57 3.5 Annonaceae Annona coriacea
## 3 1 3 5.09 4 Lauraceae Ocotea minarum
## 4 1 4 5.25 4 Lauraceae Ocotea minarum
## 5 1 5 11.8 4 Ebenaceae Diospyros hispida
## 6 1 6 7.96 5.5 Fabaceae Copaifera langsdorfii
## 7 1 7 8.91 4.5 Sapindaceae Matayba elaegnoides
## 8 1 8 5.89 3.5 Ebenaceae Diospyros hispida
## 9 1 9 8.75 4.5 Ebenaceae Diospyros hispida
## 10 1 10 4.77 2.5 Melastomataceae Miconia sp1
## # ℹ 531 more rows# Carrega pacote necessário para as análises
library(vegan)
# Gera matriz de frequência das espécies
matriz_freq <- xtabs(~Parcela+Espécie, dados)
# Pacotes para geração da tabela em HTML
library(knitr)
library(kableExtra)
library(dplyr)
# Visualizar 6 primeiras linhas (parcelas) da matriz de frequência
kable(matriz_freq[1:6,])%>%
kable_styling(fixed_thead = T)| Alibertia edulis | Anadenanthera falcata | Andira cuiabensis | Annona coriacea | Annona crassiflora | Bauhinia rufa | Bauhinia ungulata | Buchenavia tomentosa | Byrsonima basiloba | Byrsonima coccolobifolia | Byrsonima pachyphylla | Byrsonima verbascifolia | Calliandra sp1 | Campomanesia adamantium | Caryocar brasiliense | Casearia sylvestris | Connarus suberosus | Copaifera langsdorfii | Couepia grandiflora | Curatella americana | Dimorphandra mollis | Diospyros hispida | Dipteryx alata | Eriotheca gracilipes | Erythroxylum suberosum | Eugenia aurata | Eugenia punicifolia | Handroanthus albus | Himenaea courbaril | Indeterminada 1 | Indeterminada 2 | Kielmeyera coriacea | Lafoensia pacari | Leptolobium elegans | Machaerium acutifoium | Magonia pubescens | Matayba elaegnoides | Miconia sp1 | Myrcia sp1 | Ocotea minarum | Ouratea hexasperma | Ouratea spectabilis | Pouteria ramiflora | Pouteria torta | Psidium laruotteanum | Qualea grandiflora | Qualea parviflora | Rhamnidium elaeocarpum | Roupala montana | Schefflera macrocarpa | Syagrus flexuosa | Tabebuia aurea | Tachigali aurea | Tapirira guianensis | Terminalia argentea | Vatairea macrocarpa | Vochysia cinnamomea | Xylopia aromatica |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 4 | 0 | 3 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 2 | 0 | 0 | 0 | 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 4 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 4 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 7 | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
# Curva acumulação de espécies
par(mfrow=c(1,1),mar=c(4,4,2,2))
curva_acum <- specaccum(matriz_freq)
plot(curva_acum,
ci.type="polygon",
ci.col="lightgray",
ci.lty = 0,
lwd=2,
lty=2,
xlab="Unidades amostrais",
ylab="Riqueza",
main="Curva de acumulação de espécies")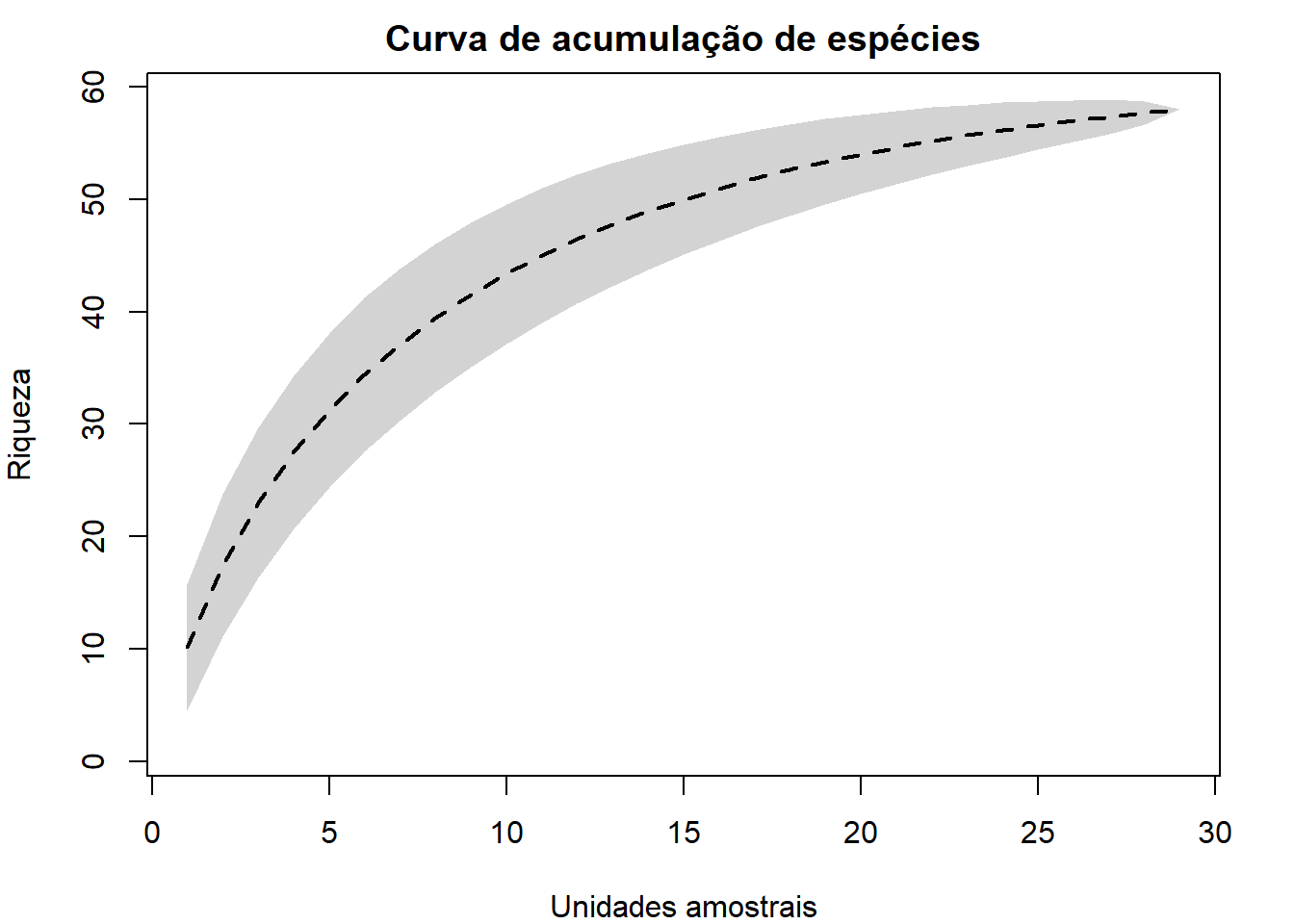
A interpretação mais trivial para a curva do coletor é que quando esta se estabiliza, formando um patamar, foi atingida a suficiência amostral para a comunidade em questão.
A riqueza representada em uma amostragem depende do esforço amostral, mais especificamente do número de indivíduos amostrados, que varia entre parcelas. Por isso, a comparação da riqueza de dois locais cujo o número de indivíduos amostrados é diferente é uma abordagem inadequada. Deste modo, para que possamos comparar a riqueza, é necessária a utilização de um denominador comum, que deve ser um número igual ou menor que o número de indivíduos amostrados nos locais. Este procedimento é conhecido como rarefação, que sumariamente consiste em gerar uma relação entre o número esperado de espécies para uma certa quantidade de indivíduos em uma ou mais amostras.
A função rarecurve do vegan retorna a riqueza esperada para um mesmo número de indivíduos, conforme o procedimento a seguir.
# Curva de rarefação
rarecurve(matriz_freq,
xlab = "Indivíduos amostrados",
ylab="Riqueza esperada",
main="Curvas de rarefação",
lty = 2)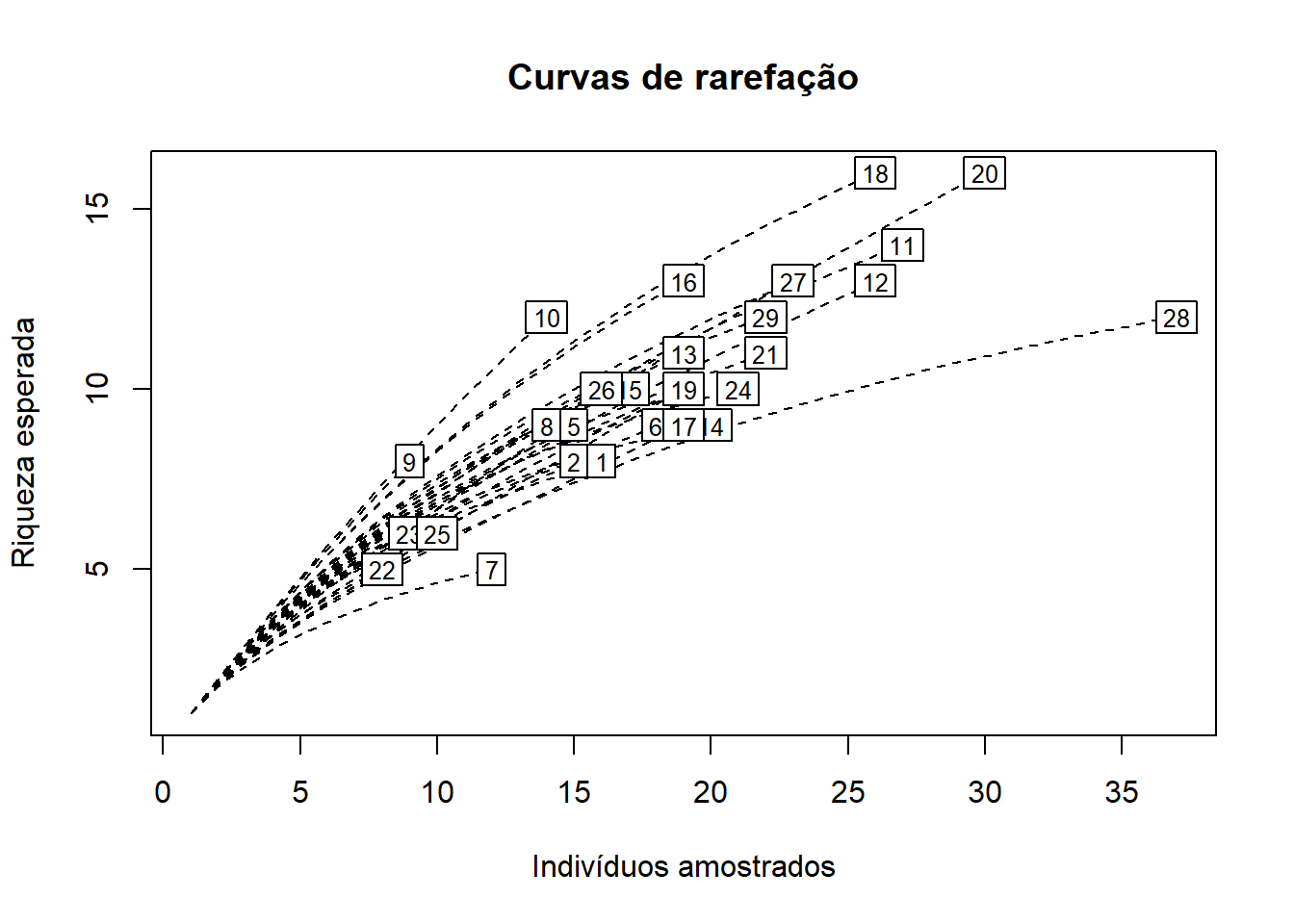
O gráfico gerado nos indica que nas parcelas de número 9, 10, 18 e 16, cujas curvas de rarefação se encontram acima das demais, podemos esperar maior riqueza de espécies para um mesmo número de indivíduos amostrados, em comparação às demais unidades amostrais.