Função de Weibull com 3 parâmetros bitruncada para representação da estrutura diamétrica de povoamentos florestais

Última atualização em Jun 8, 2023 0 Comments Biometria

Contextualização

A estrutura diamétrica, representada pela distribuição do número de árvores por hectare de uma floresta por classes de diâmetro (DAP), traz importantes informações que subsidiam o diagnóstico e/ou as ações de manejo a serem realizadas em um povoamento/comunidade florestal.

A distribuição diamétrica é comumente representada por funções de densidade de probabilidade, sendo a de Weibull uma das mais difundidas para esta finalidade. Esta função possui diferentes variações em sua formulação, podendo apresentar 2 ou 3 parâmetros, e ainda ser truncada à direita, esquerda ou bitruncada.

As variações truncadas são empregadas quando são conhecidos limites superiores e/ou inferiores da distribuição. Neste post empregaremos a função de distribuição probabilística de Weibull bitruncada para representação da estrutura diamétrica de um povoamento florestal que possui os DAPs máximos e mínimos conhecidos ao longo do tempo.

Modelagem dos atributos do povoamento

Para o exemplo deste post, vamos trabalhar com dados de mensurações em quatro parcelas permanentes. Começamos pela importação dos dados, e pela análise visual dos dados de diâmetro ao longo do tempo.

library(dplyr)
library(ggplot2)

# importar os dados
dados <- readr::read_csv2('https://raw.githubusercontent.com/sergiocostafh/open_data/main/cinv_example_proc.csv')

# ver a estrutura dos dados
glimpse(dados)

## Rows: 32
## Columns: 9
## $ Parcela  <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3…
## $ Idade    <dbl> 6.212183, 8.213552, 9.147159, 12.002738, 13.251198, 14.403833…
## $ DAP      <dbl> 13.67579, 17.25158, 17.98280, 20.90473, 21.15867, 21.60449, 2…
## $ DAPmin   <dbl> 5.50000, 6.10000, 10.30000, 12.73240, 12.73240, 13.05100, 13.…
## $ DAPmax   <dbl> 18.90000, 24.40000, 26.30000, 31.83099, 32.46761, 34.30000, 3…
## $ Hdom     <dbl> 9.514286, 12.942857, 13.942857, 18.200000, 19.971429, 20.9285…
## $ N        <dbl> 1305.3037, 1305.3037, 1277.8236, 1222.9291, 1222.9291, 1222.9…
## $ G        <dbl> 19.70139, 31.49424, 33.42807, 43.49868, 44.66113, 46.80353, 4…
## $ VolTotal <dbl> 90.50862, 180.87759, 204.67636, 341.30509, 386.07986, 433.945…

# calcular o diametro quadratico das parcelas a partir da area basal
dados <- dados %>% 
  mutate(Dg = sqrt((G/N)*40000/pi))

# visualizar as medicoes subsequentes
ggplot(dados)+
  geom_line(aes(x = Idade, y = DAP, color = 'DAP médio'))+
  geom_line(aes(x = Idade, y = DAPmin, color = 'DAP mínimo'))+
  geom_line(aes(x = Idade, y = DAPmax, color = 'DAP máximo'))+
  geom_line(aes(x = Idade, y = Dg, color = 'Diâmetro quadrático'))+
  labs(x = 'Idade (anos)',
       y = 'Diâmetro (cm)',
       title = 'Crescimento em diâmetro quadrático, DAP médio, mínimo e máximo',
       subtitle = 'Avaliação contínua em 4 parcelas permanentes de Pinus sp.')+
  scale_color_brewer(palette = 'Set1')+
  facet_wrap(~Parcela)+
  theme_minimal()+
  theme(
    plot.title.position = 'plot',
    legend.title = element_blank(),
        legend.position = 'bottom'
    )

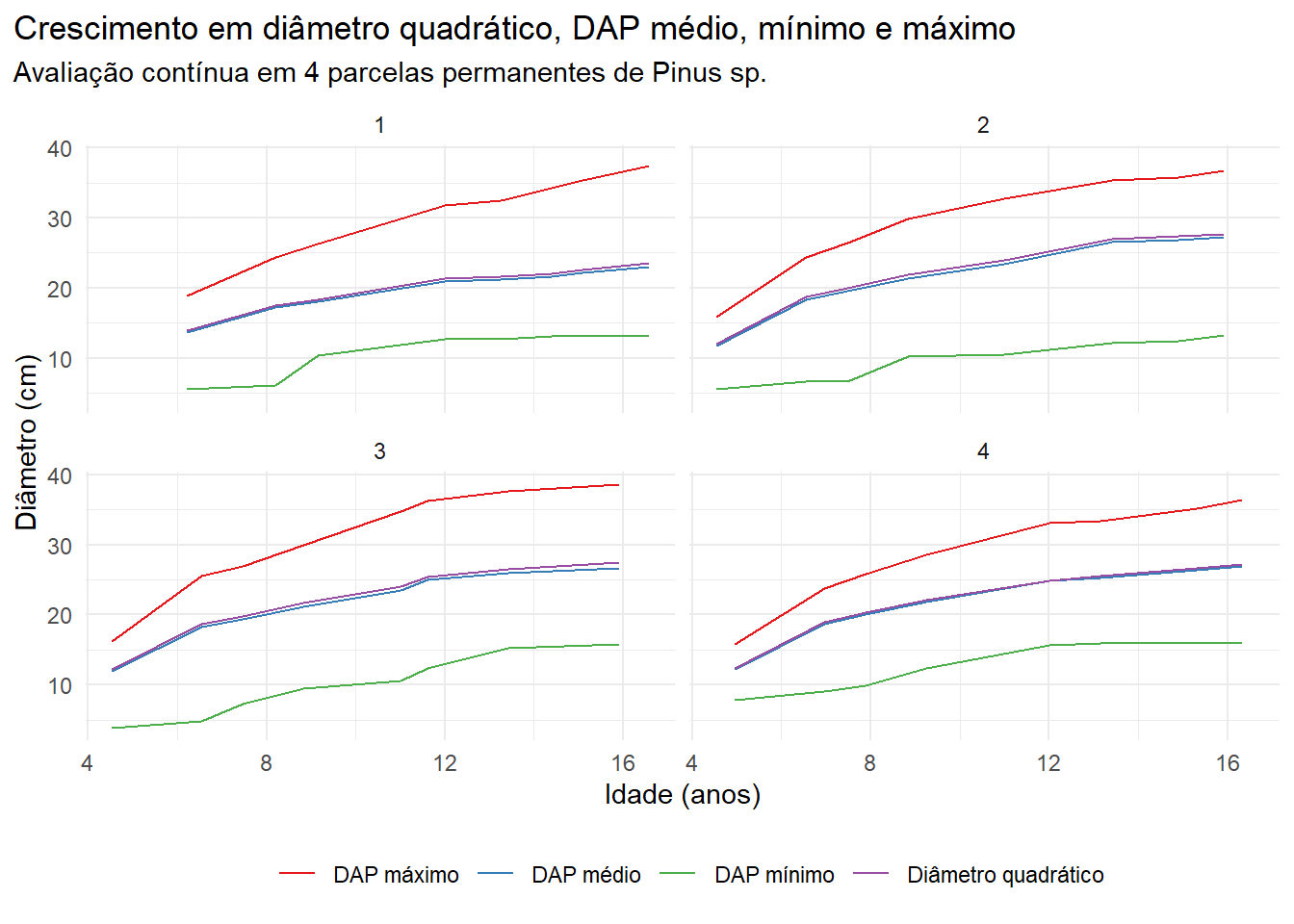Considerando que estas parcelas são todas pertencentes a um mesmo povoamento, vamos ajustar modelos que descrevem o comportamento médio das variáveis apresentadas no tempo. Usaremos o modelo de Chapman-Richards.

library(minpack.lm)

# modelo de crescimento em dap
dap_model <- nlsLM(DAP ~ a * (1-exp(-b*Idade))^c,
      data = dados,
      start = list (a = 30, b = .5, c = 1.5))

# modelo de crescimento em dap minimo
dapmin_model <- nlsLM(DAPmin ~ a * (1-exp(-b*Idade))^c,
                   data = dados,
                   start = list (a = 30, b = .5, c = 1.5))

# modelo de crescimento em dap maximo
dapmax_model <- nlsLM(DAPmax ~ a * (1-exp(-b*Idade))^c,
                   data = dados,
                   start = list (a = 30, b = .5, c = 1.5))

# modelo de crescimento em diametro quadratico
dg_model <- nlsLM(Dg ~ a * (1-exp(-b*Idade))^c,
                      data = dados,
                      start = list (a = 30, b = .5, c = 1.5))

Na sequência, vamos analisar visualmente o comportamento dos modelos em relação aos pontos observados.

library(tidyr)

# criar tabela para predicoes ao longo do tempo
dados_pred <- tibble(Idade = seq(4,17,1)) %>% 
  mutate(DAP = predict(dap_model, .),
         DAPmin = predict(dapmin_model, .),
         DAPmax = predict(dapmax_model, .),
         Dg = predict(dg_model, .)) %>% 
  pivot_longer(DAP:Dg)

# formatar tabela de dados para visualizacao
dados_plot <- dados %>% 
  select(Idade, DAP, DAPmin, DAPmax, Dg) %>% 
  pivot_longer(DAP:Dg)

# visualizar dados observados e estimativas
ggplot(mapping = aes(x = Idade, y = value, color = name))+
  geom_point(data = dados_plot)+
  geom_line(data = dados_pred)+
  labs(x = 'Idade (anos)',
       y = 'Diâmetro (cm)',
       title = 'Crescimento em diâmetro quadrático, DAP médio, mínimo e máximo',
       subtitle = 'Avaliação contínua em 4 parcelas permanentes de Pinus sp.')+
  scale_color_brewer(palette = 'Set1')+
  scale_x_continuous(limits = c(0,20))+
  theme_minimal()+
  theme(
    plot.title.position = 'plot',
    legend.title = element_blank(),
    legend.position = 'bottom'
  )

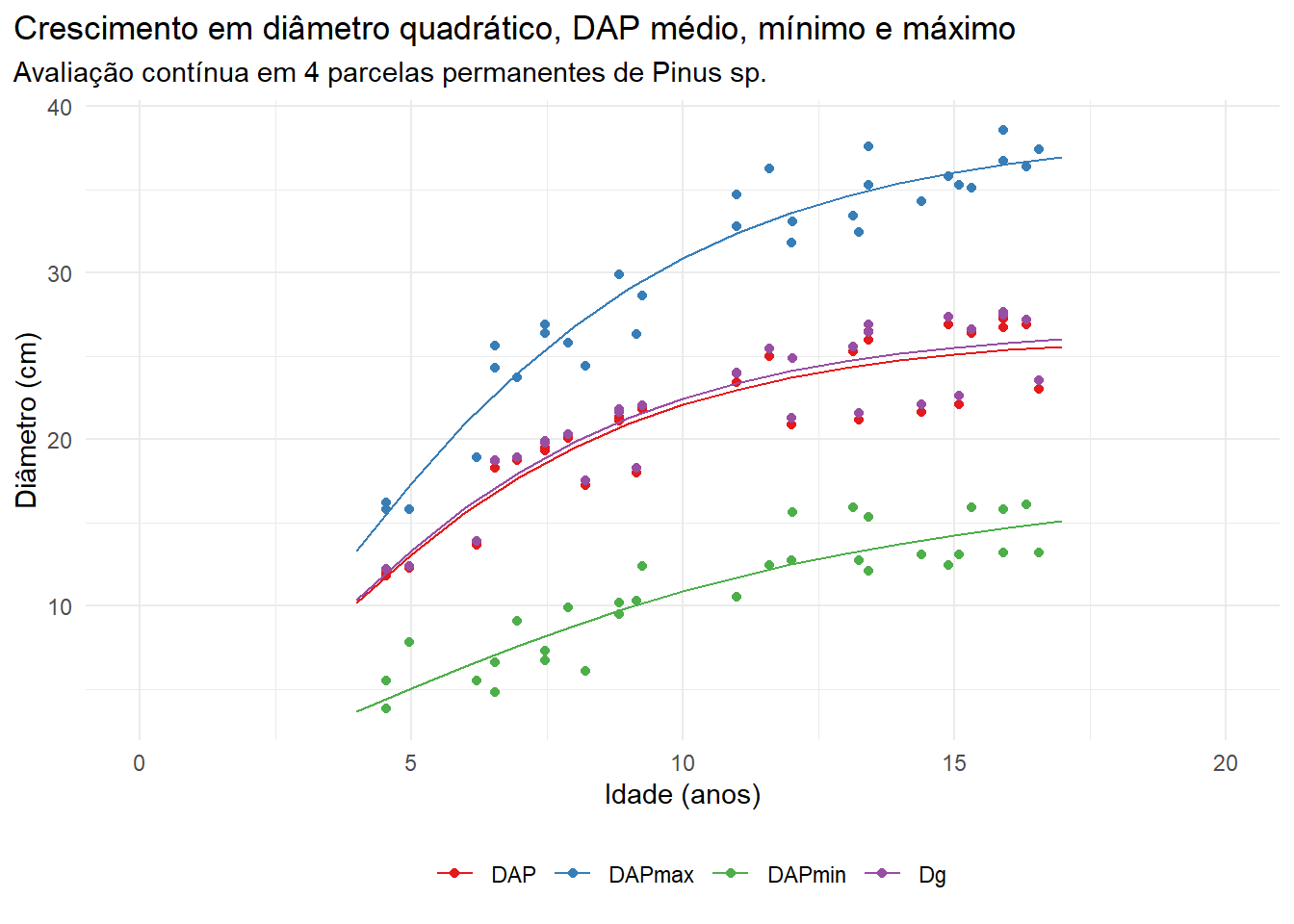
Constata-se que os modelos apresentam o comportamento adequado para representar os diferentes tipos de diâmetros que queremos modelar. Poderíamos testar outros modelos e indicadores de qualidade de ajuste para escolher a melhor equação, mas não é o nosso objetivo agora.
Agora que já podemos obter os diâmetros quadrático, médio, mínimo e máximo em qualquer momento no tempo, seguiremos para a etapa de obtenção da estrutura diamétrica.

Função bitruncada de Weibull com 3 parâmetros

Primeiro, vamos às formulações. A função bitruncada de densidade de probabilidade de Weibull com 3 parâmetros é expressa matematicamente da seguinte maneira:

$\frac{\frac{c}{b} {(\frac{x - a}{b})}^{c - 1} e x p [{(\frac{t - a}{b})}^{c} - {(\frac{x - a}{b})}^{c}]}{1 - e x p [- {(\frac{T - a}{b})}^{c}]}$

Em que:

a: parâmetro de locação;
b: parâmetro de escala;
c: parâmetro de forma;
x: variável aleatória (DAP ou classe de DAP);
T: ponto de truncamento à direita (DAP máximo);
t: ponto de truncamento à esquerda (DAP mínimo).

Obteremos os parâmetros a, b, e c da função pelo método dos momentos não centrais, conforme o estudo de Arce (2004). Para tal, as seguintes expressões devem ser usadas.

Parâmetro a:
$a = \frac{\overset{―}{d} - (d g - D_{m i n})}{1 - \frac{1}{n^{(1 + \frac{1}{c})}}}$ Parâmetro b:
$b = [\frac{\overset{―}{d} - d_{m i n}}{Γ (1 + \frac{1}{c})}] [1 - \frac{1}{n^{(1 + \frac{1}{c})}}]$
Parâmetro c:
$d g^{2} = {\overset{―}{d}}^{2} + {(\overset{―}{d} - d_{m i n})}^{2} [\frac{\frac{Γ (1 + \frac{2}{c})}{Γ (1 + \frac{1}{c})^{2}} - 1}{{[1 - {\frac{1}{n}}^{(1 + \frac{1}{c})}]}^{2}}]$ O parâmetro c pode ser obtida por um técnica iterativa, desde que conhecidos os valores para as demais variáveis da função. A partir do parâmetro c, podem ser obtidos os valores de a e b por substituição nas respectivas fórmulas.

Agora vamos aplicar o que foi descrito. Começamos pela implementação das fórmulas.

# funcao para obtencao do parametro a
a_function <- function(dap, dg, dapmin, c, n){(dap-(dg-dapmin))/(1-(1/n^(1+1/c)))}

# funcao para obtencao do parametro b
b_function <- function(dap, dapmin, c, n){((dap-dapmin)/gamma(1+1/c))*(1-1/(n^1+1/c))}

# funcao para obtencao do parametro c
c_function <- function (dap, dg, dapmin, c, n){
  ((dap^2+(dap-dapmin)^2*((gamma(1+2/c)/(gamma(1+1/c)^2)-1)/(1-(1/n)^(1+1/c))^2))-dg^2)^2
}

# funcao bitruncada de Weibull com 3 paramentros
weibull3p_bitr <- function(x, a, b, c, dapmin, dapmax){
  ((c/b)*(((x-a)/b)^(c-1))*
     exp((((dapmin-a)/b)^c)-(((x-a)/b)^c)))/
    (1-exp(-((dapmax-a)/b)^c))
}

Na sequência iremos aplicar as funções que declaramos acima para obtenção dos parâmetros a, b e c da função de Weibull. Podemos utilizar a função optimize para obter o parâmetro c. Observe que declaramos a equação de um modo que c é o valor que zero o resultado da equação. Da maneira a qual iremos declarar, c deverá um valor entre 0 e 100 que minimiza (de preferência, zere) o resultado da função c_function.
O aninhamento da base de dados (função nest) por idade em conjunto com a função map do pacote purrr, nos fornecem a estrutura necessária para obter o parâmetro c pra cada linha (idade) da base de dados.
Um dos parâmetros necessários para calcularmos o número de árvores por classe diamétrica, é o próprio número de árvores total do povoamento. Como aqui não trabalharemos com um modelo de sobrevivência, vamos assumir 1000 árvores por hectare em todas as idades, apenas para fins de exemplo.

library(purrr)

# numero de arvores por hectare
narv <- 1000

# aplicar as funcoes na tabela de predicoes para obtencao dos parametros a, b, e c
dados_pred <- dados_pred %>% 
  group_by(Idade) %>%
  pivot_wider(names_from = name, values_from = value) %>% 
  nest() %>% 
  mutate(
    c = map(.x = data, 
            ~optimize(
              c_function,
              lower = 0, upper = 100, 
              tol = .001,
              dap = .x$DAP,
              dg = .x$Dg,
              dapmin = .x$DAPmin,
              n = narv
            )$minimum)
  ) %>% 
  unnest(c(data, c)) %>% 
  mutate(
    a = a_function(DAP,Dg,DAPmin,c,narv),
    b = b_function(DAP,DAPmin,c,narv)
  )

# visualizar as primeiras linhas da base de dados
head(dados_pred)

## # A tibble: 6 × 8
## # Groups:   Idade [6]
##   Idade   DAP DAPmin DAPmax    Dg     c     a     b
##   <dbl> <dbl>  <dbl>  <dbl> <dbl> <dbl> <dbl> <dbl>
## 1     4  10.2   3.67   13.3  10.4  3.84  3.49  7.21
## 2     5  13.1   5.03   17.4  13.3  3.67  4.80  8.94
## 3     6  15.6   6.36   21.0  15.9  3.51  6.09 10.3 
## 4     7  17.8   7.63   24.1  18.1  3.35  7.32 11.3 
## 5     8  19.5   8.81   26.8  19.8  3.21  8.47 11.9 
## 6     9  20.9   9.88   29.0  21.3  3.08  9.52 12.3

Agora que temos os parâmetros da função de Weibull do povoamento em diferentes momentos no tempo, podemos construir a distribuição diamétrica média de cada idade aplicando a função bitruncada de Weibull com três parâmetros.

# criar classes de dap
classes_dap <- 1:50

# criar base de dados para construcao da estrutura diametrica em cada idade
dist_diam_pred <- dados_pred %>% 
  group_by(Idade) %>% 
  nest() %>% 
  mutate(
    dist = map(.x = data, ~weibull3p_bitr(classes_dap, .x$a, .x$b, .x$c, .x$DAPmin, .x$DAPmax) * narv)
  ) %>% 
  unnest(c(data, dist)) %>% 
  mutate(cdap = classes_dap) 

# visualizar estrutura diametrica ao longo do tempo
ggplot(dist_diam_pred)+
  geom_line(aes(x = cdap, y = dist, group = Idade, color = Idade))+
  labs(x = 'DAP (cm)',
       y = 'Frequência (n/ha)',
       title = 'Distribuição diamétrica de um povoamento de Pinus sp. dos 4 aos 17 anos de idade')+
  scale_color_viridis_c(name = 'Idade (anos)')+
  theme_minimal()+
  theme(
    plot.title.position = 'plot',
    legend.position = 'right'
  )

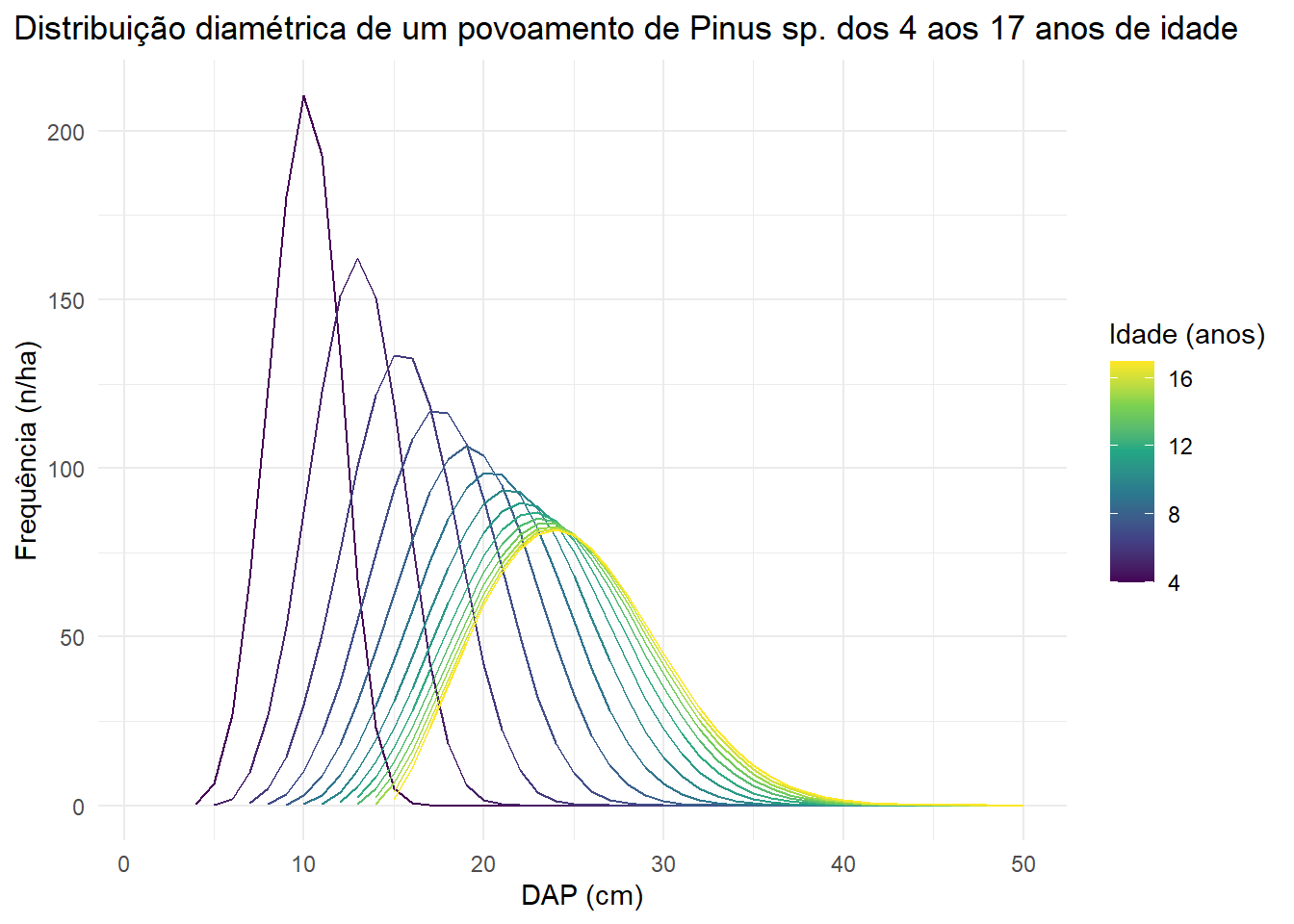
O gráfico apresentado demonstra a flexibilidade da função de Weibull para representar a estrutura diamétrica de povoamentos florestais equiâneos em qualquer momento no tempo. Uma abordagem mais aprimorada envolve a aplicação de um modelo de sobrevivência para estimativa do número de árvores esperada em cada idade, a partir de uma densidade inicial.

Distribuição Probabilística Crescimento e Produção Biometria

Sérgio Costa

MSc. Engenheiro Florestal

Mestre em Engenharia Florestal pela Universidade Federal do Paraná, atualmente trabalha como Especialista em Modelagem de Dados na Arauco Forest Brasil.