Funções de afilamento de forma fixa e variável

Última atualização em Mar 25, 2019 0 Comments Biometria

Na mensuração florestal, funções de afilamento de forma fixa são as mais difundidas devido à facilidade em seu ajuste e aplicação. O procedimento de integração exigido para obtenção dos volumes a diferentes alturas também é facilitado pelo uso desse tipo de função. Tradicionalmente, são mais utilizadas as funções polinomiais, como o modelo de Schöepfer (1966) e de Hradetzky (1976), descritos matematicamente pelas seguintes expressões.

Modelo de Schöepfer (1966)

$\frac{d_{i}}{d a p} = β_{0} \frac{h_{i}}{h t} + β_{1} {\frac{h_{i}}{h t}}^{2} + β_{2} {\frac{h_{i}}{h t}}^{3} + β_{3} {\frac{h_{i}}{h t}}^{4} + β_{4} {\frac{h_{i}}{h t}}^{5}$

Modelo de Hradetzky (1976)

$\frac{d_{i}}{d a p} = β_{0} \frac{h_{i}}{h t} + β_{1} {\frac{h_{i}}{h t}}^{p_{1}} + β_{2} {\frac{h_{i}}{h t}}^{p_{2}} + . . . + β_{n} {\frac{h_{i}}{h t}}^{p_{n}}$

em que:
$β_{1}, β_{2}, . . ., β_{n}$ = parâmetros do modelo;
$p_{1}, p_{2}, . . ., p_{n}$ = parâmetros selecionados pelo procedimento stepwise; $h_{i}$ = altura até a seção i do fuste;
$d_{i}$ = diâmetro na seção i do fuste;
$d a p$ = diãmetro à altura do peito;
$h t$ = altura total.

As funções de afilamento de forma variável, introduzidas por Kozak (1988) e Newnham (1988), possuem como principal vantagem a capacidade de modelar diferentes formas de árvore em função de características dendrométricas, tornando possível a utilização de uma única equação de afilamento para árvores em diferentes idades e de diferentes portes. A utilização desta técnica permite a redução do número de funções de afilamento ajustados considerando povoamentos de uma mesma espécie estabelecidos em momentos e condições distintas. Neste exercício testaremos o modelo de Kozak (2004) e a função trigonométrica de Bi (2000) como representantes desta categoria de modelos.

Modelo de Kozak (2004)

$d_{i} = β_{0} d a p^{β_{1}} {[\frac{1 - {(\frac{h_{i}}{h t})}^{1 / 4}}{1 - p^{1 / 4}}]}^{β_{2} + β_{3} (\frac{1}{e^{d a p / h t}}) + β_{4} d a p^{[\frac{1 - {(\frac{h_{i}}{h t})}^{1 / 4}}{1 - p^{1 / 4}}]} + β_{5} {[\frac{1 - {(\frac{h_{i}}{h t})}^{1 / 4}}{1 - p^{1 / 4}}]}^{d a p / h t}}$ em que:
$p$ = primeiro ponto de inflexão calculado no modelo segmentado de Max e Burkhart (1976). Obs: neste exercício, será tratado como mais uma parâmetro a ser ajustado.

Modelo de Bi (2000)

$d_{i} = d a p [{(\frac{l o g s i n (\frac{π}{2} \frac{h_{i}}{h t})}{l o g s i n (\frac{π}{2} \frac{1, 3}{h t})})}^{β_{0} + β_{1} s i n (\frac{π}{2} \frac{h_{i}}{h t}) + β_{2} s i n (\frac{3 π}{2} \frac{h_{i}}{h t}) + β_{3} s i n (\frac{π}{2} \frac{h_{i}}{h t}) / \frac{h_{i}}{h t} + β_{4} d a p + β_{5} \frac{h_{i}}{h t} \sqrt{d a p} + β_{6} \frac{h_{i}}{h t} \sqrt{h t}}]$

Para praticar o ajuste dos modelos, vamos importar um conjunto de dados de cubagens.

# Importar dados
library(readxl)
dados <- read_excel('dados_cubagens.xlsx')
dados

## # A tibble: 54,415 × 7
##    ARVORE   DAP    DI     HI    HT `HI/HT` `DI/DAP`
##     <dbl> <dbl> <dbl>  <dbl> <dbl>   <dbl>    <dbl>
##  1      1 0.600 1.91  0.0735  1.47  0.05       3.18
##  2      1 0.600 1.59  0.1     1.47  0.0680     2.65
##  3      1 0.600 1.59  0.147   1.47  0.1        2.65
##  4      1 0.600 1.27  0.221   1.47  0.15       2.12
##  5      1 0.600 1.27  0.3     1.47  0.204      2.12
##  6      1 0.600 1.27  0.368   1.47  0.25       2.12
##  7      1 0.600 1.27  0.515   1.47  0.35       2.12
##  8      1 0.600 0.955 0.662   1.47  0.45       1.59
##  9      1 0.600 0.955 0.7     1.47  0.476      1.59
## 10      1 0.600 0.955 0.809   1.47  0.55       1.59
## # ℹ 54,405 more rows

summary(dados)

##      ARVORE          DAP              DI               HI         
##  Min.   :   1   Min.   : 0.60   Min.   : 0.000   Min.   : 0.0735  
##  1st Qu.: 840   1st Qu.:11.80   1st Qu.: 5.411   1st Qu.: 0.8315  
##  Median :1688   Median :18.10   Median :12.096   Median : 3.0600  
##  Mean   :1688   Mean   :18.39   Mean   :13.455   Mean   : 5.5745  
##  3rd Qu.:2534   3rd Qu.:23.90   3rd Qu.:19.735   3rd Qu.: 8.8200  
##  Max.   :3369   Max.   :56.70   Max.   :72.256   Max.   :33.1300  
##        HT            HI/HT              DI/DAP      
##  Min.   : 1.47   Min.   :0.003018   Min.   :0.0000  
##  1st Qu.: 8.79   1st Qu.:0.074244   1st Qu.:0.4310  
##  Median :14.26   Median :0.350000   Median :0.8402  
##  Mean   :14.23   Mean   :0.396116   Mean   :0.7572  
##  3rd Qu.:19.40   3rd Qu.:0.750000   3rd Qu.:1.0459  
##  Max.   :33.13   Max.   :1.000000   Max.   :3.8197

# Plotar dispersão da relação hi/ht x di/dap
plot(`DI/DAP`~`HI/HT`, data = dados,
     xlab = 'hi/ht', ylab = 'di/dap')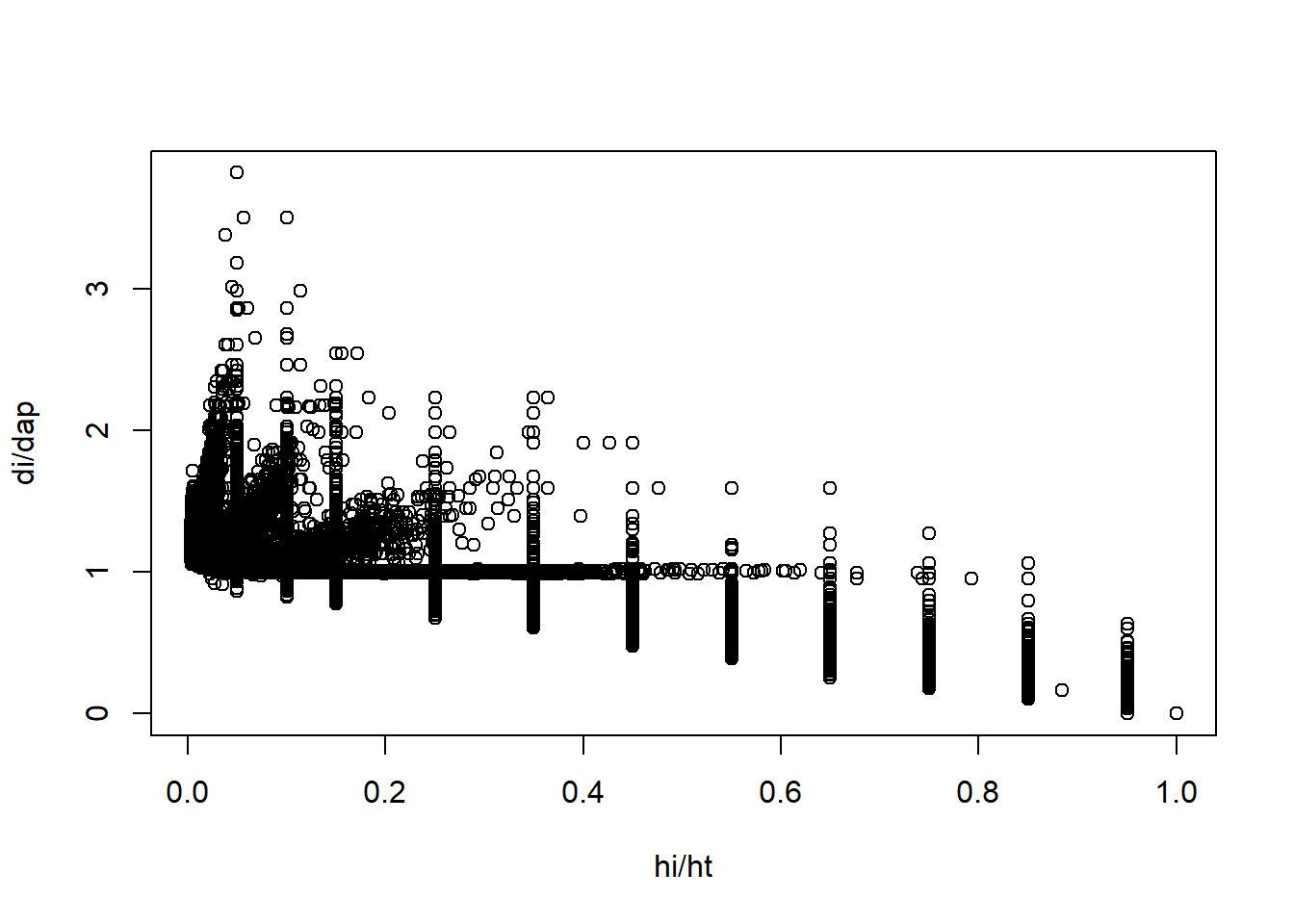

# Plotar dispersão da relação dap x ht
plot(HT~DAP, data = dados,
     xlab = 'DAP (cm)', ylab = 'Ht (m)')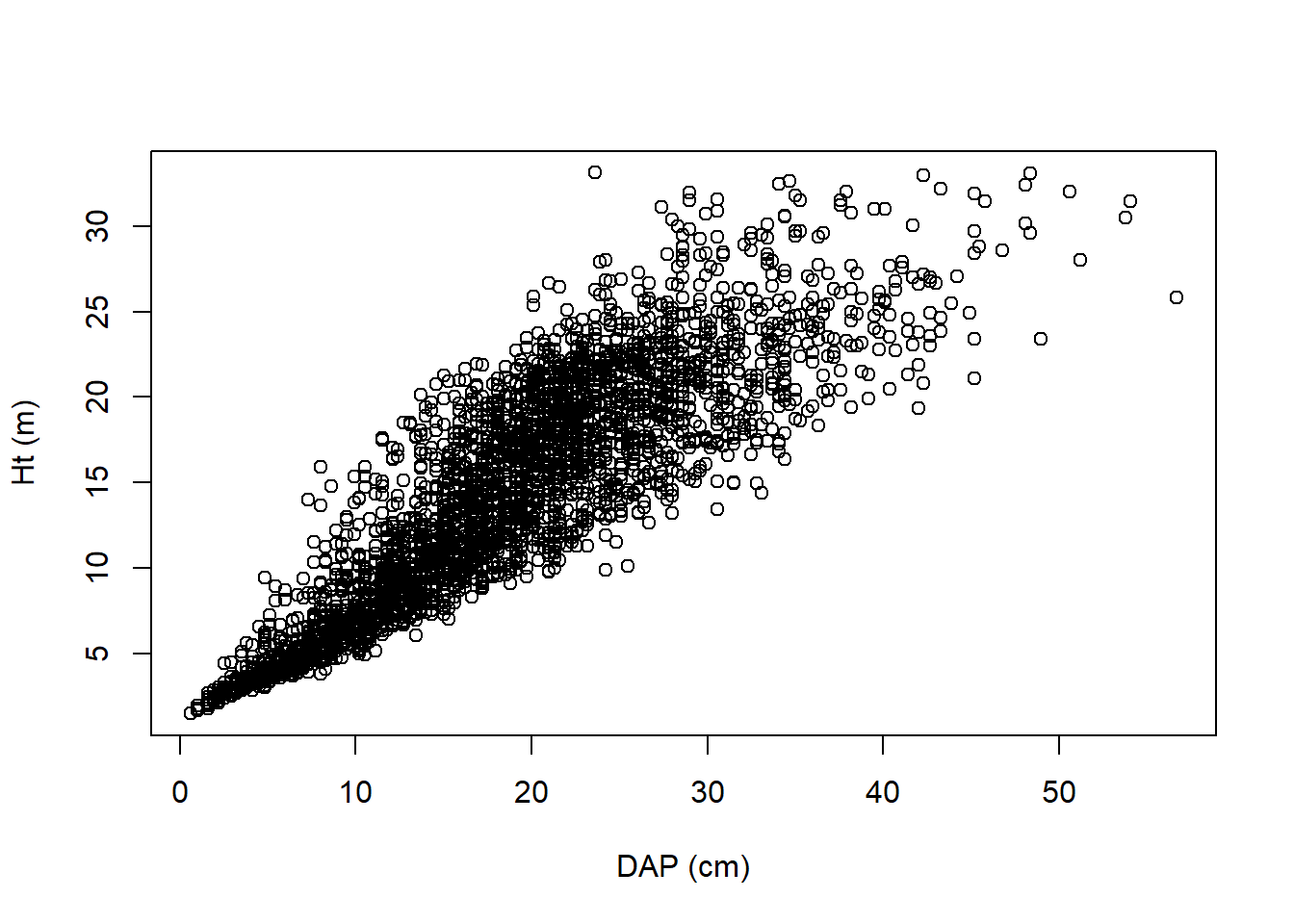

A base carregada consiste em dados de cubagens de 3.369 árvores, que tiveram diâmetros medidos a alturas relativas (5%, 10%, 15%, 25%, 35%, 45%, 55%, 65%, 75%, 85% e 95%), e também a alturas fixas (0,1, 0,3, 0,7 e 1,30 m).

Foram cubadas árvores de 0,6 a 56,7 cm de DAP, com alturas variando entre 1,47 e 33,13 m, indicando uma elevada variabilidade de portes de árvores.

Para utilização de funções polinomiais ou outras de forma fixa, é necessária a estratificação dos dados visando a redução da variabilidade existente. Neste caso, deverá ser gerada uma função de afilamento para cada estrato. Neste exemplo vamos estratificar o conjunto de dados a partir do DAP, sendo que o primeiro grupo compreenderá as árvores com menos de 5cm de dap e os demais serão formados com intervalos de 10 cm.

# Gerar as classes
dados$classe_dap <- cut(dados$DAP,
                          breaks = c(0,c(5,15,25,35,45,Inf)))
# Resumir as classes
summary(dados$classe_dap)

##    (0,5]   (5,15]  (15,25]  (25,35]  (35,45] (45,Inf] 
##     2992    17072    22495     9744     1808      304

Agora iremos ajustar o modelo de Schöepfer para cada um dos grupos.

# Criar uma lista para armazenar os modelos
funcoes_schoepfer <- list()
# Ajustar um modelo para cada grupo
for(i in levels(dados$classe_dap)){
funcoes_schoepfer[[i]] <- lm(`DI/DAP`~`HI/HT`+I(`HI/HT`^2)+I(`HI/HT`^3)+I(`HI/HT`^4)+I(`HI/HT`^5), data = subset(dados,dados$classe_dap==i))
}
# Resumo dos resultados dos modelos
lapply(funcoes_schoepfer, summary)

## $`(0,5]`
## 
## Call:
## lm(formula = `DI/DAP` ~ `HI/HT` + I(`HI/HT`^2) + I(`HI/HT`^3) + 
##     I(`HI/HT`^4) + I(`HI/HT`^5), data = subset(dados, dados$classe_dap == 
##     i))
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.66404 -0.13447 -0.03705  0.07904  2.09370 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    1.92582    0.02667  72.209  < 2e-16 ***
## `HI/HT`       -4.70643    0.55981  -8.407  < 2e-16 ***
## I(`HI/HT`^2)  16.05552    3.46957   4.628 3.86e-06 ***
## I(`HI/HT`^3) -39.11067    8.78035  -4.454 8.72e-06 ***
## I(`HI/HT`^4)  43.79063    9.62348   4.550 5.57e-06 ***
## I(`HI/HT`^5) -17.91781    3.79077  -4.727 2.39e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2528 on 2986 degrees of freedom
## Multiple R-squared:  0.8186,	Adjusted R-squared:  0.8183 
## F-statistic:  2694 on 5 and 2986 DF,  p-value: < 2.2e-16
## 
## 
## $`(5,15]`
## 
## Call:
## lm(formula = `DI/DAP` ~ `HI/HT` + I(`HI/HT`^2) + I(`HI/HT`^3) + 
##     I(`HI/HT`^4) + I(`HI/HT`^5), data = subset(dados, dados$classe_dap == 
##     i))
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.36353 -0.06147 -0.01085  0.04006  0.87430 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    1.379487   0.003302  417.77   <2e-16 ***
## `HI/HT`       -3.688856   0.077362  -47.68   <2e-16 ***
## I(`HI/HT`^2)  14.704332   0.517705   28.40   <2e-16 ***
## I(`HI/HT`^3) -36.228895   1.369753  -26.45   <2e-16 ***
## I(`HI/HT`^4)  39.094052   1.541516   25.36   <2e-16 ***
## I(`HI/HT`^5) -15.249265   0.617510  -24.70   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1055 on 17066 degrees of freedom
## Multiple R-squared:  0.9396,	Adjusted R-squared:  0.9396 
## F-statistic: 5.313e+04 on 5 and 17066 DF,  p-value: < 2.2e-16
## 
## 
## $`(15,25]`
## 
## Call:
## lm(formula = `DI/DAP` ~ `HI/HT` + I(`HI/HT`^2) + I(`HI/HT`^3) + 
##     I(`HI/HT`^4) + I(`HI/HT`^5), data = subset(dados, dados$classe_dap == 
##     i))
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.23163 -0.03199 -0.00084  0.02766  0.48511 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    1.246046   0.001145 1087.90   <2e-16 ***
## `HI/HT`       -4.071009   0.030005 -135.68   <2e-16 ***
## I(`HI/HT`^2)  17.476210   0.208070   83.99   <2e-16 ***
## I(`HI/HT`^3) -38.933380   0.561174  -69.38   <2e-16 ***
## I(`HI/HT`^4)  37.991111   0.639011   59.45   <2e-16 ***
## I(`HI/HT`^5) -13.708137   0.257950  -53.14   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.05219 on 22489 degrees of freedom
## Multiple R-squared:  0.981,	Adjusted R-squared:  0.9809 
## F-statistic: 2.316e+05 on 5 and 22489 DF,  p-value: < 2.2e-16
## 
## 
## $`(25,35]`
## 
## Call:
## lm(formula = `DI/DAP` ~ `HI/HT` + I(`HI/HT`^2) + I(`HI/HT`^3) + 
##     I(`HI/HT`^4) + I(`HI/HT`^5), data = subset(dados, dados$classe_dap == 
##     i))
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.20115 -0.03189  0.00065  0.02693  0.35102 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    1.216174   0.001565  776.87   <2e-16 ***
## `HI/HT`       -4.202002   0.043583  -96.41   <2e-16 ***
## I(`HI/HT`^2)  18.609030   0.305483   60.92   <2e-16 ***
## I(`HI/HT`^3) -40.530337   0.825602  -49.09   <2e-16 ***
## I(`HI/HT`^4)  38.157955   0.940584   40.57   <2e-16 ***
## I(`HI/HT`^5) -13.252322   0.379751  -34.90   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.05069 on 9738 degrees of freedom
## Multiple R-squared:  0.9816,	Adjusted R-squared:  0.9815 
## F-statistic: 1.036e+05 on 5 and 9738 DF,  p-value: < 2.2e-16
## 
## 
## $`(35,45]`
## 
## Call:
## lm(formula = `DI/DAP` ~ `HI/HT` + I(`HI/HT`^2) + I(`HI/HT`^3) + 
##     I(`HI/HT`^4) + I(`HI/HT`^5), data = subset(dados, dados$classe_dap == 
##     i))
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.142770 -0.027460 -0.002403  0.022018  0.257885 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    1.200521   0.003163  379.56   <2e-16 ***
## `HI/HT`       -4.266131   0.091633  -46.56   <2e-16 ***
## I(`HI/HT`^2)  18.779570   0.647795   28.99   <2e-16 ***
## I(`HI/HT`^3) -39.872610   1.753872  -22.73   <2e-16 ***
## I(`HI/HT`^4)  36.363012   1.998715   18.19   <2e-16 ***
## I(`HI/HT`^5) -12.208106   0.806897  -15.13   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.0463 on 1802 degrees of freedom
## Multiple R-squared:  0.9846,	Adjusted R-squared:  0.9845 
## F-statistic: 2.303e+04 on 5 and 1802 DF,  p-value: < 2.2e-16
## 
## 
## $`(45,Inf]`
## 
## Call:
## lm(formula = `DI/DAP` ~ `HI/HT` + I(`HI/HT`^2) + I(`HI/HT`^3) + 
##     I(`HI/HT`^4) + I(`HI/HT`^5), data = subset(dados, dados$classe_dap == 
##     i))
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.122237 -0.031020  0.003504  0.025404  0.166978 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    1.191807   0.007745 153.874  < 2e-16 ***
## `HI/HT`       -4.527408   0.231443 -19.562  < 2e-16 ***
## I(`HI/HT`^2)  20.094868   1.650086  12.178  < 2e-16 ***
## I(`HI/HT`^3) -42.661480   4.478459  -9.526  < 2e-16 ***
## I(`HI/HT`^4)  38.969213   5.107729   7.629 3.20e-13 ***
## I(`HI/HT`^5) -13.070928   2.062564  -6.337 8.63e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.04846 on 298 degrees of freedom
## Multiple R-squared:  0.9834,	Adjusted R-squared:  0.9832 
## F-statistic:  3539 on 5 and 298 DF,  p-value: < 2.2e-16

Para ajustar o modelo de Kozak, vamos utilizar a função nlsLM do pacote minpack.LM. Esta função busca parâmetros de modelos não lineares empregando o algoritmo Levenberg-Marquadt e costuma ser mais eficiente que a função nls, especialmente quando buscamos ajustar modelos mais complexos.

library(minpack.lm)
# Ajuste do modelo de Kozak
kozak <- nlsLM(DI~b0*(DAP^b1)*((1-(HI/HT)^(1/4))/(1-p^(1/4)))^(b2+b3*(1/exp(DAP/HT))+b4*DAP^((1-(HI/HT)^(1/4))/(1-p^(1/4)))+b5*((1-(HI/HT)^(1/4))/(1-p^(1/4)))^(DAP/HT)),
data = dados,
start=list(b0=1,b1=1,b2=1,b3=-1,b4=0.00001,b5=-0.01, p = 0.3))
summary(kozak)

## 
## Formula: DI ~ b0 * (DAP^b1) * ((1 - (HI/HT)^(1/4))/(1 - p^(1/4)))^(b2 + 
##     b3 * (1/exp(DAP/HT)) + b4 * DAP^((1 - (HI/HT)^(1/4))/(1 - 
##     p^(1/4))) + b5 * ((1 - (HI/HT)^(1/4))/(1 - p^(1/4)))^(DAP/HT))
## 
## Parameters:
##      Estimate Std. Error t value Pr(>|t|)    
## b0  1.129e+00  6.062e-03  186.26   <2e-16 ***
## b1  8.896e-01  9.135e-04  973.88   <2e-16 ***
## b2  6.994e-01  2.313e-03  302.40   <2e-16 ***
## b3 -6.180e-01  6.870e-03  -89.95   <2e-16 ***
## b4  2.752e-06  3.284e-07    8.38   <2e-16 ***
## b5 -3.390e-02  9.240e-04  -36.69   <2e-16 ***
## p   2.868e-01  4.167e-03   68.83   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.248 on 54408 degrees of freedom
## 
## Number of iterations to convergence: 10 
## Achieved convergence tolerance: 1.49e-08

#Ajuste do modelo de Bi
bi = nlsLM(DI ~ DAP*(log(sin((pi/2)*(HI/HT)))/(log(sin((pi/2)*(1.3/HT)))))**
  (b0+b1*sin((pi/2)*(HI/HT))+b2*cos((3*pi/2)*(HI/HT))+b3*(sin((pi/2)*(HI/HT))/(HI/HT))+
     b4*DAP+b5*(HI/HT)*DAP**0.5+b6*(HI/HT)*HT**0.5),
data=dados,
start=c(b0=1.8,b1=-0.2,b2=-0.04,b3=-0.9,b4=-0.0006,b5=0.07,b6=-.14))
summary(bi)

## 
## Formula: DI ~ DAP * (log(sin((pi/2) * (HI/HT)))/(log(sin((pi/2) * (1.3/HT)))))^(b0 + 
##     b1 * sin((pi/2) * (HI/HT)) + b2 * cos((3 * pi/2) * (HI/HT)) + 
##     b3 * (sin((pi/2) * (HI/HT))/(HI/HT)) + b4 * DAP + b5 * (HI/HT) * 
##     DAP^0.5 + b6 * (HI/HT) * HT^0.5)
## 
## Parameters:
##      Estimate Std. Error t value Pr(>|t|)    
## b0  1.801e+00  1.212e-02  148.65   <2e-16 ***
## b1 -2.803e-01  6.123e-03  -45.78   <2e-16 ***
## b2 -5.107e-02  1.565e-03  -32.62   <2e-16 ***
## b3 -9.142e-01  7.134e-03 -128.14   <2e-16 ***
## b4 -8.873e-04  5.188e-05  -17.10   <2e-16 ***
## b5  7.406e-02  1.161e-03   63.79   <2e-16 ***
## b6 -1.277e-01  9.892e-04 -129.13   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9302 on 54408 degrees of freedom
## 
## Number of iterations to convergence: 4 
## Achieved convergence tolerance: 1.49e-08

Agora que temos as funções de forma fixa e variável ajustadas, vamos comparar os métodos. Para tal, precisamos armazenar os resíduos em vetores e calcular o erro quadrático médio em relação ao $d_{i}$ .

# Criar conjuntos que armazenarão os resultados das funções de Schoepfer
di_schoepfer <- c()
residuos_schoepfer <- c()
# Calcular os resíduos a partir das funções de Schoepfer
for(i in unique(dados$classe_dap)){
di_schoepfer <- append(di_schoepfer,predict(funcoes_schoepfer[[i]])*subset(dados$DAP,dados$classe_dap==i))
residuos_schoepfer <- append(residuos_schoepfer,subset(dados$DI,dados$classe_dap==i)-predict(funcoes_schoepfer[[i]])*subset(dados$DAP,dados$classe_dap==i))}
# Resíduos da função de Kozak e Bi
residuos_kozak <- residuals(kozak)
residuos_bi <- residuals(bi)
# Calcular o erro quadrático médio
eqm_schoepfer <- sqrt(sum(residuos_schoepfer^2)/nrow(dados))
eqm_kozak <- sqrt(sum(residuos_kozak^2)/nrow(dados))
eqm_bi <- sqrt(sum(residuos_bi^2)/nrow(dados))
# Calcular o erro quadrático médio percentual
eqm_perc_schoepfer <- eqm_schoepfer/mean(dados$DI)*100
eqm_perc_kozak <- eqm_kozak/mean(dados$DI)*100
eqm_perc_bi <- eqm_bi/mean(dados$DI)*100
# Plotar resultados
par(mfrow=c(1,3))
plot(residuos_schoepfer~di_schoepfer,
     main = paste('Schoepfer - EQM% = ', round(eqm_perc_schoepfer,2)),
     xlab = 'Di estimado', ylab = 'Resíduos',
     ylim = c(-15,15))+
  lines(x=c(0,70),y=c(0,0))
plot(residuos_kozak~dados$DI,
     main = paste('Kozak - EQM% = ', round(eqm_perc_kozak,2)),
     xlab = 'Di estimado', ylab = 'Resíduos',
     ylim = c(-15,15))+
  lines(x=c(0,70),y=c(0,0))
plot(residuos_bi~dados$DI,
     main = paste('Bi - EQM% = ', round(eqm_perc_bi,2)),
     xlab = 'Di estimado', ylab = 'Resíduos',
     ylim = c(-15,15))+
  lines(x=c(0,70),y=c(0,0))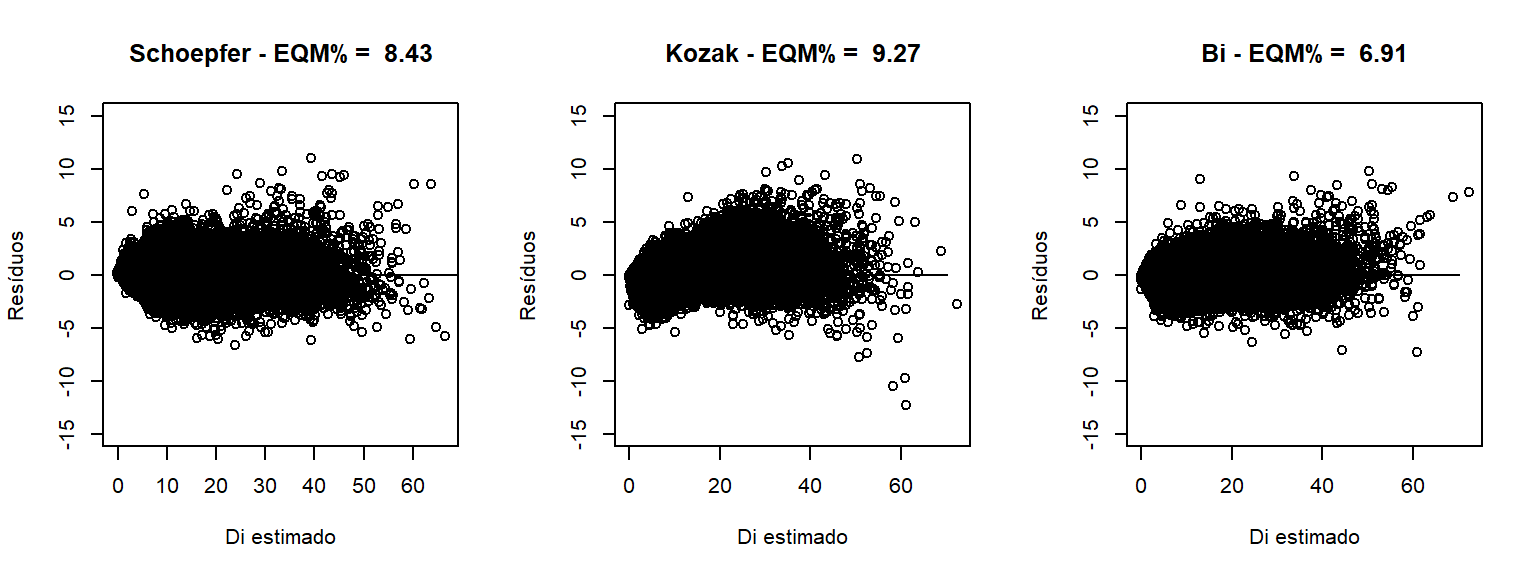

O modelo trigonométrico de Bi superou os demais tanto pelo menor erro quadrático médio, quanto pela dispersão de resíduos mais homogeneamente distribuída ao longo da linha de ajuste.
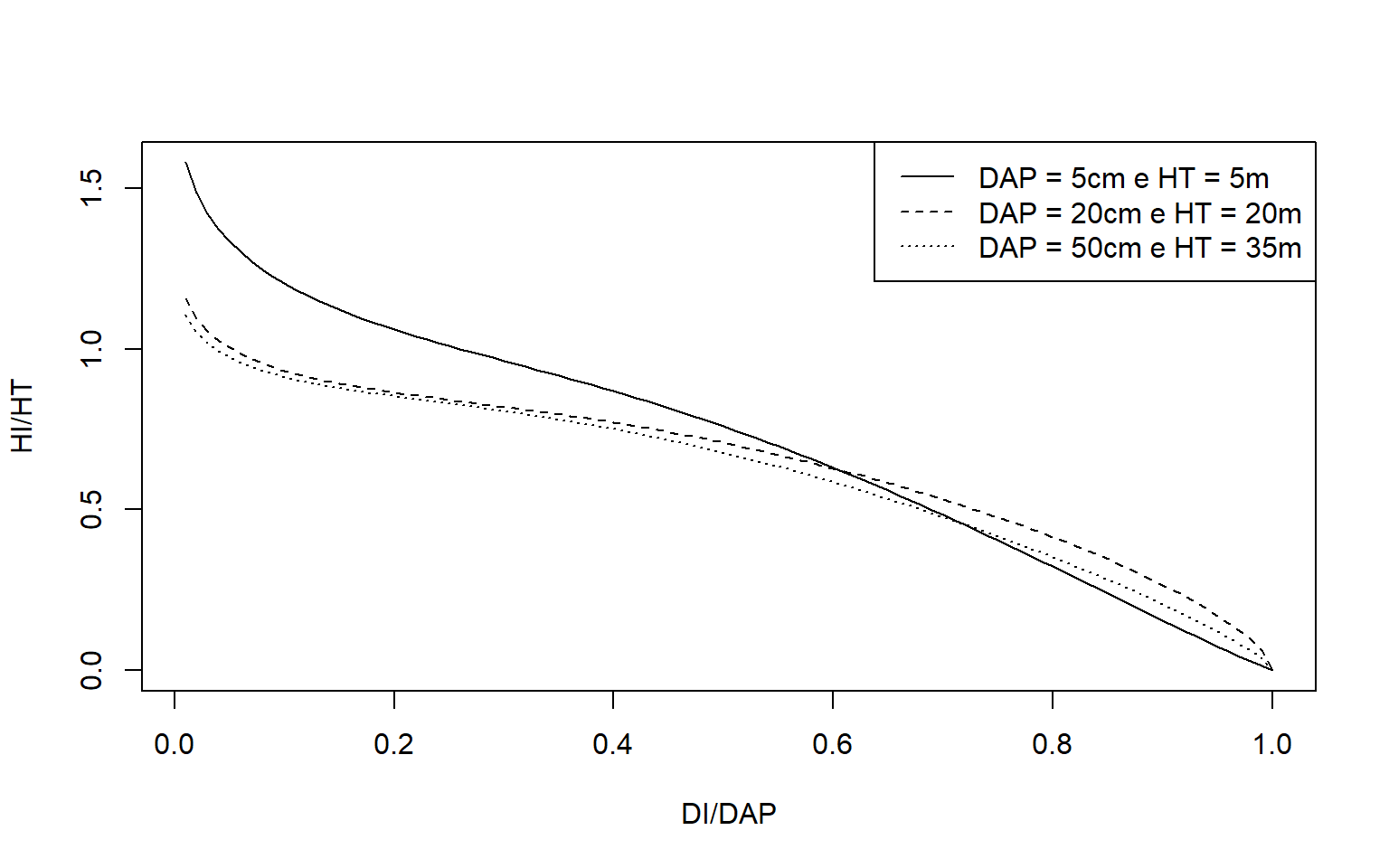
Por fim, vamos visualizar a capacidade da equação gerada a partir do modelo de Bi em descrever diferentes formas de fuste.

# Simular dados de árvores de diferentes portes
arvores_simuladas <- data.frame(DAP = rep(c(5,20,50),each = 100),
                                HT = rep(c(5,25,35),each = 100),
                                `HI/HT` = seq(0.01,1,0.01))
arvores_simuladas$HI <- arvores_simuladas$HI.HT*arvores_simuladas$HT
# Aplicar a equação ajustada de Bi aos dados simulados
arvores_simuladas$DI <- predict(bi,arvores_simuladas)
# Plotar curvas de afilamento
lt <- 1
plot(I(DI/DAP)~I(HI/HT),subset(arvores_simuladas, arvores_simuladas$DAP==unique(arvores_simuladas$DAP)[1]), type = 'l', lty = lt,
             xlab ='DI/DAP', ylab = 'HI/HT')+
for (i in unique(arvores_simuladas$DAP)[-1]) {
  lt <- lt+1
  lines(I(DI/DAP)~I(HI/HT),
        subset(arvores_simuladas,arvores_simuladas$DAP==i), lty = lt)
}
    legend('topright', legend= c('DAP = 5cm e HT = 5m', 'DAP = 20cm e HT = 20m', 'DAP = 50cm e HT = 35m'),
           lty = 1:3)

Biometria Afilamento

Sérgio Costa

MSc. Engenheiro Florestal

Mestre em Engenharia Florestal pela Universidade Federal do Paraná, atualmente trabalha como Especialista em Modelagem de Dados na Arauco Forest Brasil.