Modelagem global para prognose da produção florestal
Para definição do regime de manejo a ser adotado em um empreendimento florestal o conhecimento do fluxo de produção potencial é fundamental. A geração dessa informação a partir de uma base de dados pré existente exige o uso de ferramentas de modelagem estatística, que permitam simular o crescimento e a produção de povoamentos para diferentes classes de produtividade.
Podemos agrupar os métodos para prognose da produção florestal em três classes de abrangência: modelos a nível de povoamento, de classes diamétricas, e de árvores individuais.
Neste exemplo trabalharemos com modelos a nível de povoamento, também conhecidos como modelos globais, que se baseiam em características do povoamento como idade, área basal e índice de sítio, sendo os mais amplamente utilizados na modelagem do crescimento e da produção no Brasil.
Iniciaremos o procedimento de modelagem global com a importação e visualização dos dados.
# Importar conjunto de dados
dados <- readxl::read_excel('dados_processados.xlsx')
# Carrega pacote de gráficos
library(ggplot2)
# Plotar Idade x Volume
ggplot()+
geom_point(aes(x=IDADE, y=VOLTOT), data = dados, alpha = 0.3)+
xlab('Idade (anos)')+
ylab('Volume total (m³/ha)')+
scale_x_continuous(expand = c(0,0), limits = c(0,30), breaks = seq(0,30,5))+
scale_y_continuous(expand = c(0,0), limits = c(0,800))+
theme_bw()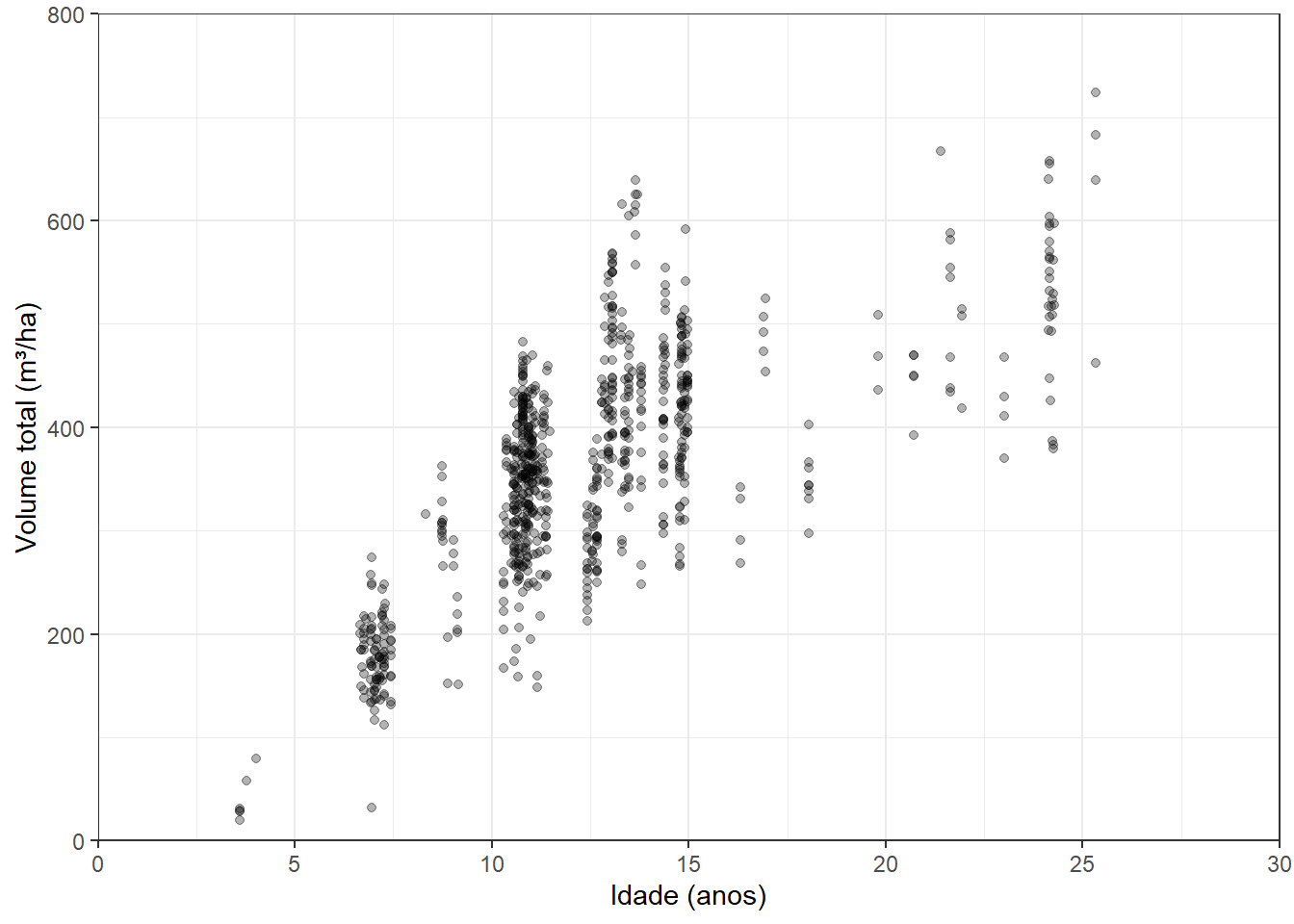
O procedimento de classificação é explicado de maneira detalhada no post Classificação de sítio florestais. Abaixo iremos apenas reproduzir o que foi desenvolvido e explicado lá.
# Carrega pacote necessário para ajuste dos modelos
library(minpack.lm)
# Ajustar modelos de Chapman-Richards para o crescimento em hdom
chapman.richards_hdom <- nlsLM(HDOM ~ a*(1-exp(-b*IDADE))^c,
data = dados,
start=list(a=30, b=0.1, c=0.8))
# Criar função de projeção
chapman.richards_hdom_proj <-function(hdom1,id2,id1){
hdom1*
((1-exp(-coef(chapman.richards_hdom)[2]*id2))/(1-exp(-coef(chapman.richards_hdom)[2]*id1)))^
coef(chapman.richards_hdom)[3]}
# Projetar a altura dominante para a idade de 15 anos (idade de referência)
dados$sitio <- chapman.richards_hdom_proj(hdom1=dados$HDOM,id2=15,id1=dados$IDADE)
#Definir o número de classes
nclasses <- 5
# Identificar a amplitude das classes de sitio
amplitude <- round(max(dados$sitio),0) - round(min(dados$sitio),0)
# Aqui diminuo a amplitude para reduzir o efeito dos extremos
amplitude <- amplitude-4
# Definir o intervalo de classe
ic <- amplitude/nclasses
# Limite inferior
li <- mean(dados$sitio)-((nclasses-1)/2*ic)-ic/2
# Definir as classes
classes <- rep(NA,nclasses)
for(i in 1:nclasses){
classes[i] <- li+i*ic-ic/2
}
classes <- round(classes,1)
# Definir os limites de classes
limites <- rep(NA,nclasses+1)
for(i in 1:(nclasses+1)){
limites[i] <- li+(i-1)*ic
}
# Classificação de sitio
dados$classe_sitio <- cut(dados$sitio,
breaks = c(-Inf,limites[-c(1,nclasses+1)],Inf),
labels = classes)Após a classificação de sítio, podemos visualizar como esta variável se relaciona com distribuição de pares de observações de idade x volume total.
plot_vol <- ggplot()+
geom_point(aes(x=IDADE, y=VOLTOT, color=factor(classe_sitio)), data = dados, alpha = 0.8)+
xlab('Idade (anos)')+
ylab('Volume total (m³/ha)')+
scale_x_continuous(expand = c(0,0), limits = c(0,30), breaks = seq(0,30,5))+
scale_y_continuous(expand = c(0,0), limits = c(0,800))+
scale_color_brewer(name='Classes de sítio', palette = 'YlOrRd')+
theme_bw()+
theme(legend.position = 'bottom')
plot_vol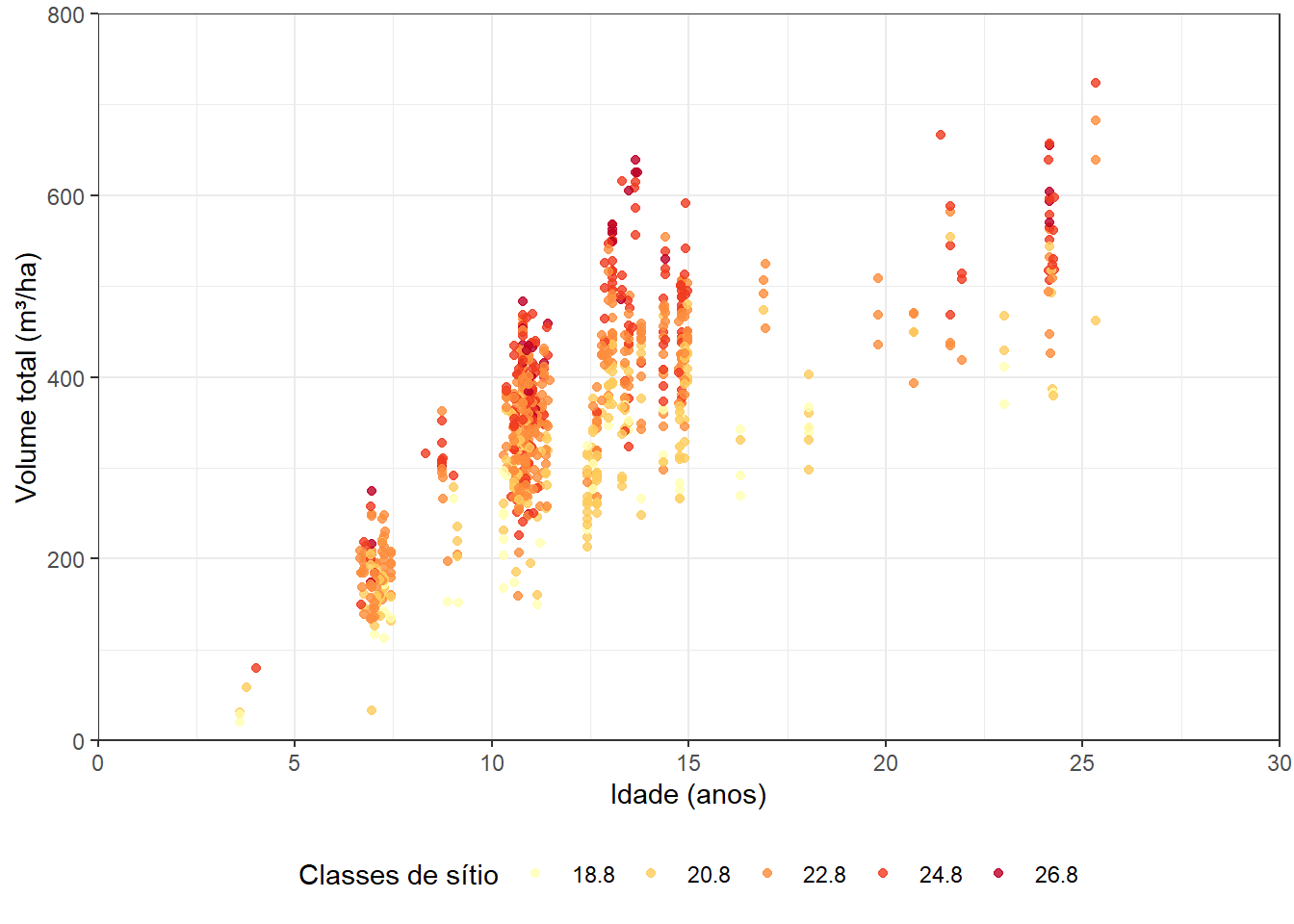
O gráfico demonstra o comportamento esperado entre sítio e produção em volume, em que povoamentos de classes superiores tendem ser mais produtivos. Vamos ajustar um modelo de produção em volume total considerando as variáveis sítio e idade.
# Ajustar modelo global de volume
chapman.richards_vol <- nlsLM(VOLTOT ~ (a+a1*sitio)*(1-exp(-b*IDADE))^c,
data = dados,
start=list(a=700, a1=1, b=0.1, c=0.8))
# Calcular erro padrão das estimativas
syx_abs_richards_v <- summary(chapman.richards_vol)$sigma
syx_abs_richards_v <- syx_abs_richards_v/mean(dados$VOLTOT)*100
# Conjunto de dados para gerar curvas de predição
idades <- 0:30
dados_predict_sitio <- data.frame(IDADE=rep(idades,times=5),
sitio=rep(classes,
each=length(idades)))
# Gerar curvas de predição
dados_predict_sitio$Vol <- round(predict(chapman.richards_vol,
dados_predict_sitio),1)
# Plotar curvas
plot_vol+
geom_line(aes(x=IDADE,
y=Vol,
linetype=factor(sitio)),
data=dados_predict_sitio, size=.5,
show.legend = FALSE)+
scale_linetype_manual(values=c('dashed','dashed','solid','dashed','dashed'))+
ggtitle(paste0('Modelo global de volume - Syx% = ',
round(syx_abs_richards_v,2)))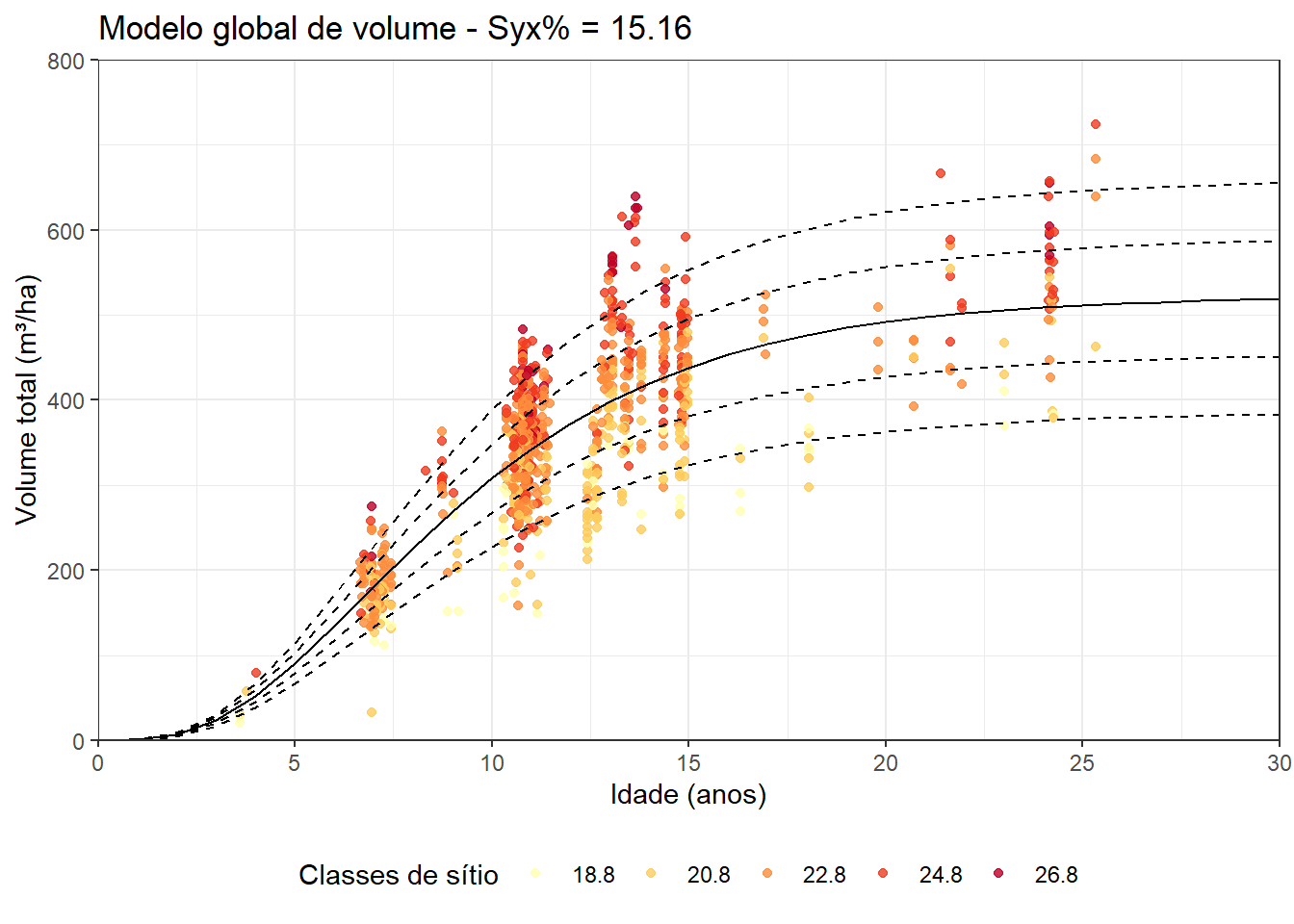
O modelo acima ajustado possui um modificador (coeficiente
Por fim, vamos visualizar a tabela de produção por classe de sítio
# Obter de produtividade dos sítios na idade de 15 anos (idade de referência)
tabela_prod <- data.frame(Idade = 0:30,
subset(dados_predict_sitio$Vol,
dados_predict_sitio$sitio==classes[1]),
subset(dados_predict_sitio$Vol,
dados_predict_sitio$sitio==classes[2]),
subset(dados_predict_sitio$Vol,
dados_predict_sitio$sitio==classes[3]),
subset(dados_predict_sitio$Vol,
dados_predict_sitio$sitio==classes[4]),
subset(dados_predict_sitio$Vol,
dados_predict_sitio$sitio==classes[5]))
colnames(tabela_prod) <- c('Idade',
paste0('Sítio ',classes[1]),
paste0('Sítio ',classes[2]),
paste0('Sítio ',classes[3]),
paste0('Sítio ',classes[4]),
paste0('Sítio ',classes[5]))
library(dplyr)
knitr::kable(tabela_prod, row.names = F, caption = 'Tabela de produção em volume total (m³/ha)')%>%
kableExtra::kable_styling(full_width = TRUE, position = "center",fixed_thead = T)| Idade | Sítio 18.8 | Sítio 20.8 | Sítio 22.8 | Sítio 24.8 | Sítio 26.8 |
|---|---|---|---|---|---|
| 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1 | 0.4 | 0.5 | 0.6 | 0.7 | 0.7 |
| 2 | 4.9 | 5.8 | 6.6 | 7.5 | 8.4 |
| 3 | 17.4 | 20.5 | 23.6 | 26.7 | 29.8 |
| 4 | 38.7 | 45.5 | 52.4 | 59.3 | 66.2 |
| 5 | 66.9 | 78.9 | 90.8 | 102.7 | 114.6 |
| 6 | 99.5 | 117.2 | 134.9 | 152.6 | 170.3 |
| 7 | 133.6 | 157.4 | 181.1 | 204.9 | 228.7 |
| 8 | 167.1 | 196.9 | 226.6 | 256.3 | 286.1 |
| 9 | 198.7 | 234.0 | 269.3 | 304.7 | 340.0 |
| 10 | 227.3 | 267.7 | 308.2 | 348.6 | 389.0 |
| 11 | 252.7 | 297.6 | 342.6 | 387.5 | 432.5 |
| 12 | 274.8 | 323.6 | 372.5 | 421.4 | 470.2 |
| 13 | 293.7 | 345.9 | 398.1 | 450.4 | 502.6 |
| 14 | 309.7 | 364.7 | 419.8 | 474.9 | 530.0 |
| 15 | 323.1 | 380.6 | 438.0 | 495.5 | 553.0 |
| 16 | 334.3 | 393.7 | 453.2 | 512.7 | 572.1 |
| 17 | 343.6 | 404.7 | 465.8 | 526.9 | 588.0 |
| 18 | 351.2 | 413.7 | 476.1 | 538.6 | 601.1 |
| 19 | 357.5 | 421.1 | 484.7 | 548.3 | 611.8 |
| 20 | 362.6 | 427.1 | 491.6 | 556.1 | 620.7 |
| 21 | 366.8 | 432.1 | 497.3 | 562.6 | 627.8 |
| 22 | 370.3 | 436.1 | 502.0 | 567.9 | 633.7 |
| 23 | 373.1 | 439.4 | 505.8 | 572.1 | 638.5 |
| 24 | 375.3 | 442.1 | 508.9 | 575.6 | 642.4 |
| 25 | 377.2 | 444.3 | 511.4 | 578.5 | 645.6 |
| 26 | 378.7 | 446.0 | 513.4 | 580.8 | 648.1 |
| 27 | 379.9 | 447.5 | 515.1 | 582.6 | 650.2 |
| 28 | 380.9 | 448.6 | 516.4 | 584.2 | 651.9 |
| 29 | 381.7 | 449.6 | 517.5 | 585.4 | 653.3 |
| 30 | 382.3 | 450.4 | 518.4 | 586.4 | 654.4 |
Sérgio Costa
MSc. Engenheiro Florestal
Mestre em Engenharia Florestal pela Universidade Federal do Paraná, atualmente trabalha como Especialista em Modelagem de Dados na Arauco Forest Brasil.