Abordagem Probabilística na Simulação de Desbastes

Última atualização em Jun 9, 2023 Biometria

Contextualização

O desbaste consiste na remoção de árvores de maneira seletiva e/ou sistemática de modo a favorecer o crescimento dos indivíduos remanescentes. O objetivo desta prática é a obtenção de árvores de maiores diâmetros ao fim da rotação e, consequentemente, maiores volumes de produtos da madeira de maior valor agregado. Os desbastes podem ser seletivos, sistemáticos ou ainda, uma combinação dos dois.

O desbaste seletivo consiste na remoção das árvores que possuem fustes defeituosos e daquelas que apresentam crescimento inferior em diâmetro (desbaste por baixo), afetando principalmente as menores classes de DAP. Já o desbaste sistemático consiste na remoção de linhas inteiras de plantio (geralmente a quarta ou a quinta), afetando todas as classes de diâmetro do povoamento.

Os desbastes costumam ser realizados em florestas manejadas para a produção de múltiplos produtos da madeira e podem variar quanto a intensidade, quantidade de vezes em que será realizado, idade em que será realizado e tipo (sistemático, seletivo ou ambos).

Neste exemplo vou compartilhar uma abordagem para simulação de desbastes que desenvolvi sob uma perspectiva probabilística. Procedimentos como esse (de simulação de desbastes) são apenas um dentre um conjunto de procedimentos que formam um sistema de simulação de crescimento e produção florestal por classes diamétricas.

O desbaste e as probabilidades

Para podermos simular matematicamente um processo que ocorre na realidade, precisamos traduzi-lo para uma abstração matemática. Para ser mais preciso, no contexto do desbaste, precisamos compreender os eventos probabilísticos envolvidos na remoção de certas árvores e na permanência de outras.

No caso do desbaste seletivo por baixo, costuma-se pensar que fundamentalmente serão removidas somente árvores das classes de diâmetro inferiores, o que na prática não é verdade. O objetivo dos desbastes é favorecer o crescimento das árvores remanescentes, e por isso a remoção de indivíduos precisa ser realizada de maneira adequadamente distribuída ao longo das linhas de plantio. Na prática, na execução de um desbaste seletivo que visa remover 25% das árvores de um povoamento, as linhas serão percorridas de modo a remover 1 a cada 4 árvores em sequência, e por vezes serão encontradas sequências de árvores sem defeitos e com bom desenvolvimento. Isso significa que nem sempre estaremos removendo árvores das classes inferiores ou defeituosas e que existe alguma probabilidade de árvores sadias e de classes de diâmetros maiores serem removidas em um desbaste seletivo. Obviamente, a probabilidade de uma árvore sadia de classe de diâmetro inferior ser removida é maior que a de uma árvore sadia de classe de diâmetro superior.

Para os desbastes sistemáticos, em que linhas inteiras de plantio são removidas, a conta é mais simples. Todas as classes de diâmetro possuem igual probabilidade de serem removidas.

Obtendo a distribuição diamétrica do povoamento

Para simularmos um desbaste, primeiro pecisamos conhecer a estrutura diamétrica do povoamento. Para tal, em nosso exemplo vamos usar a distribuição probabilística de Weibull para construir a distribuição de diâmetros à altura do peito, com base em dados conhecidos (ou estimados) de DAP médio, DAP mínimo, diâmetro quadrático (DG) e o número de árvores no momento do desbaste. Utilizaremos estes parâmetros do povoamento para obtermos os parâmetros a, b e c da distribuição de Weibull com três parâmetros, pelo método dos momentos não centrais. Há uma outra postagem aqui no blog que detalha os procedimentos envolvidos na aplicação deste método. Começaremos definindo as funções que precisaremos para este exemplo.

# função para recuperação do parâmetro c
c_function <- function (dap,dg,mindap,c,n){
  ((dap^2+(dap-mindap)^2*((gamma(1+2/c)/(gamma(1+1/c)^2)-1)/(1-(1/n)^(1+1/c))^2))-dg^2)^2
}

# função para recuperação do parâmetro a
a_function <- function(dap,dg,mindap,c,n){(dap-(dg-mindap))/(1-(1/n^(1+1/c)))}

# função para recuperação do parâmetro b
b_function <- function(dap,mindap,c,n){((dap-mindap)/gamma(1+1/c))*(1-1/(n^1+1/c))}

# função de densidade de probabilidade de weibull
weibull3p <- function(x,a,b,c){
  (c/b)*(((x-a)/b)^(c-1))*exp(-(((x-a)/b)^c))
}

# função de densidade de probabilidade de weibull acumulada
weibull3p_acum <- function(x,a,b,c){
  1 - exp(-((x-a)/b)^c)
}

Agora vamos obter os parâmetros da função de Weibull de um povoamento com as seguintes características:
- DAP médio = 14.1 cm
- DAP mínimo = 6.3 cm
- Área Basal = 19.7 m²/ha
- Número de árvores = 1223 árv/ha

# parâmetros conhecidos do povoamento
dap <- 14.1
dapmin <- 6.3
G <- 19.7
N <- 1233

# cálculo do dg
dg <- sqrt((G/N)*40000/pi)

# obtenção do parâmetro c
par_c <- optimize(
  c_function,
  lower = 0,
  upper = 100,
  tol = .001,
  dap = dap,
  dg = dg,
  mindap = dapmin,
  n = N
)$minimum

# obtenção do parâmetro a
par_a <- a_function(dap, dg, dapmin, par_c, N)

# obtenção do parâmetro b
par_b <- b_function(dap, dapmin, par_c, N)

# parâmetros de Weibull para a distribuição diamétrica do povoamento
c(a = par_a, b = par_b, c = par_c)
##        a        b        c 
## 6.138010 8.588648 4.080976

Com os parâmetros a, b, c em mãos, podemos construir a distribuição diamétrica do povoamento.

library(dplyr)
library(tidyr)
library(ggplot2)

# vetor de classes de diametro
classes_d <- seq(1,30,1)

# construir tabela de distribuicao diametrica
tab_distribuicao <- tibble(dap = classes_d) %>% 
  mutate(n = weibull3p(classes_d, par_a, par_b, par_c) * N) %>% 
  replace_na(list(n = 0))

# visualizar distribuicao diametrica
ggplot(tab_distribuicao, aes(x = dap, y = n))+
  geom_bar(stat = 'identity')+
  scale_x_continuous(breaks = seq(0,30,5))+
  labs(x = 'Classe de DAP (cm)',
       y = 'Frequência (árvores/ha)',
       title = 'Distribuição diamétrica do povoamento')+
  theme_minimal()+
  theme(plot.title.position = 'plot')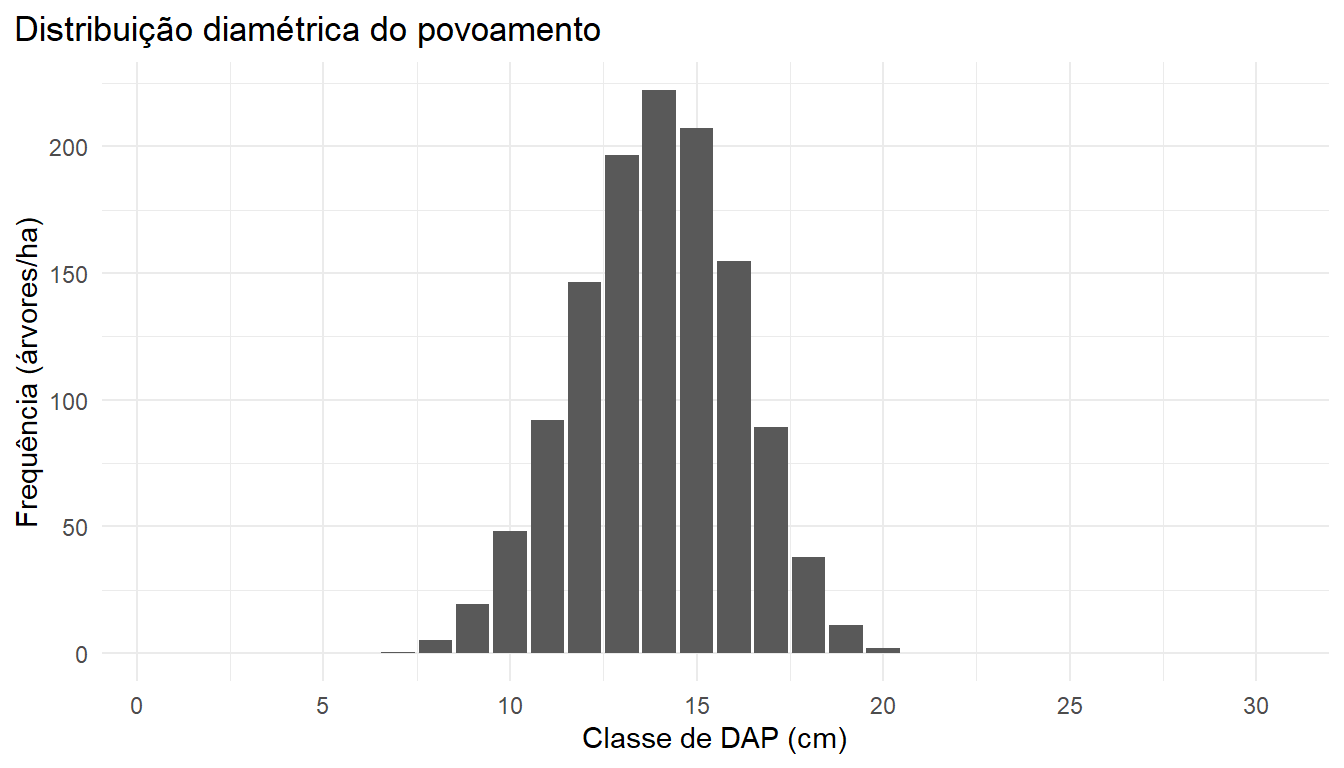

Modelando desbastes

A seguir faremos um exercício de simulação de uma intervenção em povoamento florestal que combina desbaste sistemático e seletivo.

Desbaste sistemático

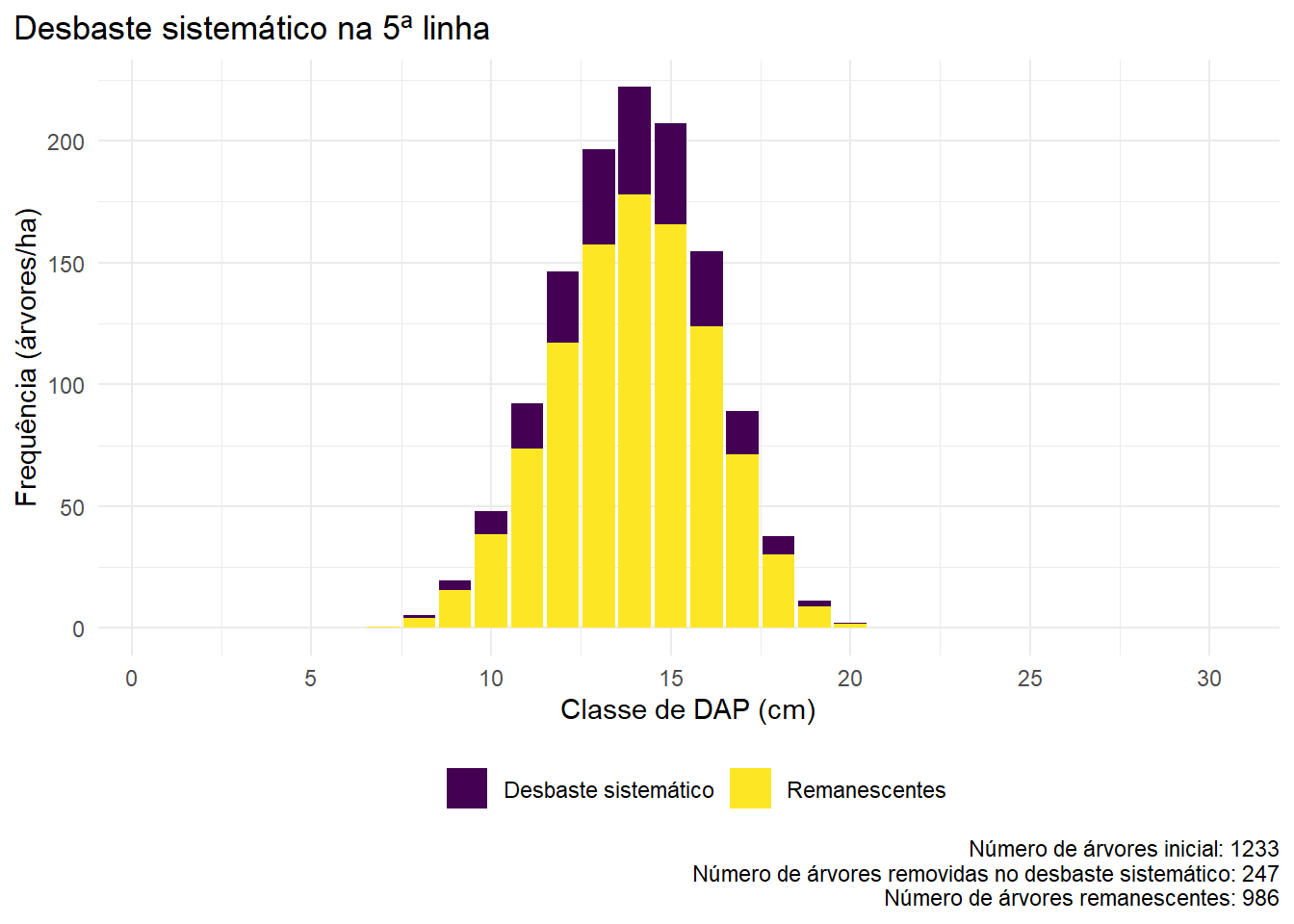
Digamos que o desbaste sistemático que queremos simular ocorrerá na quinta linha de plantio. Neste caso, estaremos removendo uma a cada cinco linhas, ou seja, 20% das árvores. Em termos de probabilidade, todas as classes de diâmetro possuem igual chance de terem representantes em uma linha desbastada, o que significa que em nossa simulação faremos um rebaixamento proporcional em todas as classes de diâmetro.

# definição da intensidade do desbaste sistemático
int_dbsist <- 1/5

# simulação de desbaste sistemático na quarta linha
tab_distribuicao <- tab_distribuicao %>% 
  # quantidade de árvores que são colhidas no desbaste sistematico
  mutate(
    `Desbaste sistemático` = n * int_dbsist
  ) %>% 
  # quantidade de árvores remanescentes
  mutate(
    `Remanescentes` = n - `Desbaste sistemático`
  )
# total de árvores colhidas no sistemático
n_colh_sist <- round(sum(tab_distribuicao$`Desbaste sistemático`))

# total de árvores remanescentes após o sistemático
n_rem_sist <- round(sum(tab_distribuicao$Remanescentes))

tab_distribuicao %>% 
  select(-n) %>% 
  pivot_longer(2:3, names_to = 'situacao', values_to = 'n') %>% 
ggplot(aes(x = dap, y = n, fill = situacao))+
  geom_bar(stat = 'identity')+
  scale_fill_viridis_d()+
  scale_x_continuous(breaks = seq(0,30,5))+
  labs(x = 'Classe de DAP (cm)',
       y = 'Frequência (árvores/ha)',
       title = 'Desbaste sistemático na 5ª linha',
       caption = paste0('Número de árvores inicial: ', N,'\n',
                        'Número de árvores removidas no desbaste sistemático: ', n_colh_sist,'\n',
                        'Número de árvores remanescentes: ', n_rem_sist))+
  theme_minimal()+
  theme(
    plot.title.position = 'plot',
    legend.position = 'bottom',
    legend.title = element_blank()
    )

Desbaste seletivo

Na simulação do desbaste seletivo é que as coisas começam a ficar mais desafiadoras. Isso porque, como já mencionado, remover apenas as árvores das classes de menor diâmetro é uma abordagem imprecisa e pouco aderente à realidade de um desbaste seletivo em campo. Vamos simular nosso desbaste seletivo de modo a restar cerca de 650 árvores por hectare. Para tal, devemos calcular a intensidade do desbaste seletivo, considerando o número de árvores remanescentes do desbaste sistemático.

# número de árvores que devem remanescer após o desbaste seletivo
nfinal <- 650

# intensidade do desbaste seletivo
int_dbsel <- (n_rem_sist - nfinal) / n_rem_sist

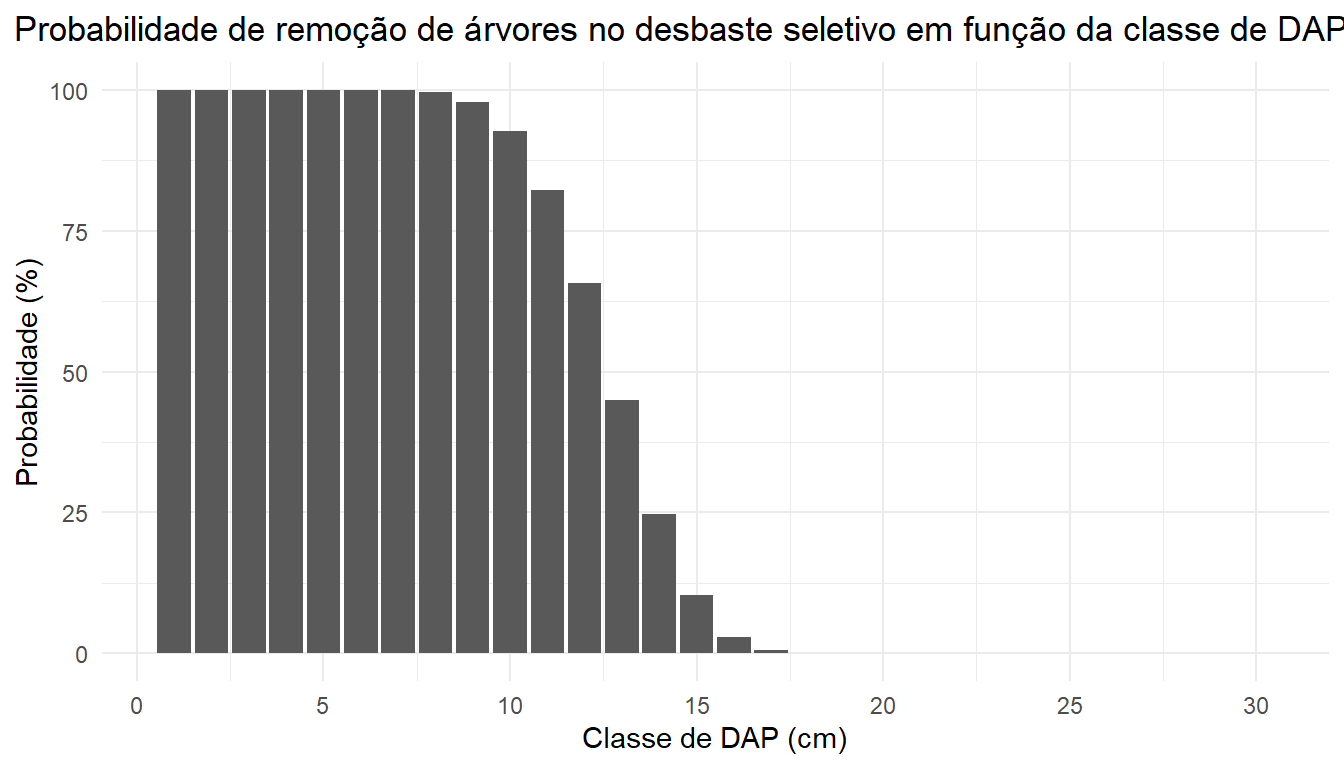
int_dbsel
## [1] 0.3407708

A intensidade calculada para chegarmos a 650 árvores por hectare é aproximadamente 1/3 árvores. Agora devemos calcular a probabilidade de uma árvore de cada classe de diâmetro ser a menor dentre 3. Para isso, devemos adotar a seguinte lógica de cálculo:
- Primeiro passo: Calcular a distribuição acumulada ao longo das classes diamétricas. Para isso podemos utilizar a fórmula da distribuição acumulada de Weibull.
- Segundo passo: Calcular a probabilidade de uma árvore sorteada da classe X ser a menor dentre 3 sorteadas. Podemos fazer isso subtraindo a probabilidade acumulada de uma árvore da classe X ser maior do que qualquer uma das outras duas árvores sorteadas (P(1) * P(2) = P²).

# intensidade do desbaste seletivo (arredondado para 1/3)
int_dbsel <- 1/3

# Calcular a probabilidade de corte no desbaste seletivo por baixo por classe de diâmetro
tab_distribuicao <- tab_distribuicao %>% 
  # calcular a distribuição cumulativa
  mutate(
    dist_acum = weibull3p_acum(dap, par_a, par_b, par_c)
    ) %>% 
  replace_na(list(dist_acum=0)) %>% 
  # calcular a probabilidade de colheita
  mutate(
    prob_colh_sel = (1-dist_acum)^(1/int_dbsel-1)
  )

ggplot(tab_distribuicao) +
  geom_bar(aes(x = dap, y = prob_colh_sel * 100 ), stat = 'identity') +
  scale_x_continuous(breaks = seq(0,30,5)) +
  labs(x = 'Classe de DAP (cm)',
       y = 'Probabilidade (%)',
       title = 'Probabilidade de remoção de árvores no desbaste seletivo em função da classe de DAP') +
  theme_minimal() +
  theme(
    plot.title.position = 'plot',
    legend.position = 'bottom',
    legend.title = element_blank()
  )

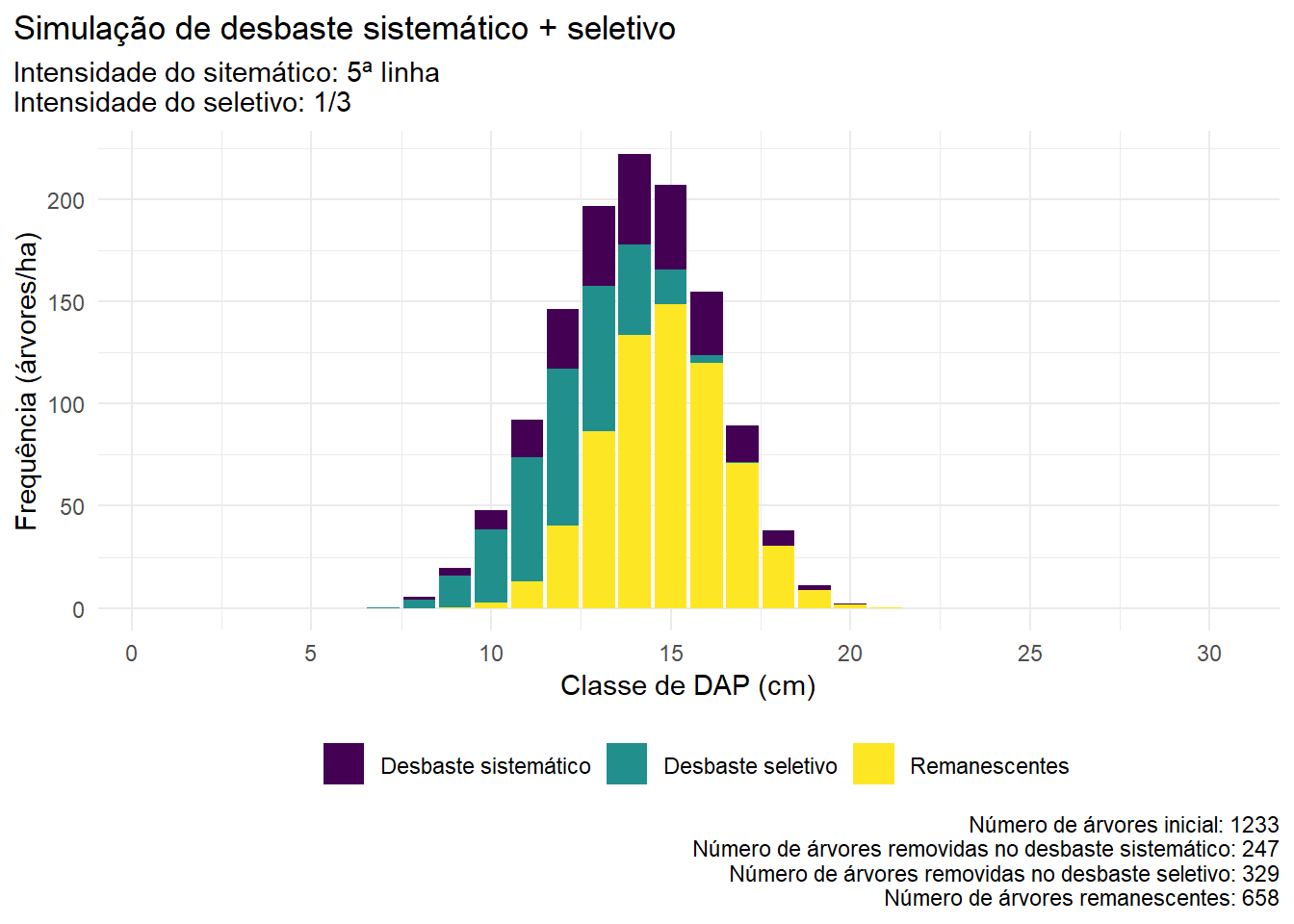
Com base nas probabilidades calculadas, podemos estimar a quantidade de árvores que serão removidas em cada classe.

tab_distribuicao <- tab_distribuicao %>% 
  # Numero de arvores a serem colhidas no desbaste seletivo
  mutate(
    `Desbaste seletivo` = Remanescentes * prob_colh_sel
    ) %>% 
  # Recalculo do numero de arvores remanescentes
  mutate(
    Remanescentes = n - (`Desbaste sistemático` + `Desbaste seletivo`)
  )


# total de árvores colhidas no seletivo
n_colh_sel <- round(sum(tab_distribuicao$`Desbaste seletivo`))

# total de árvores remanescentes após o desbaste seletivo + sistemático
n_rem_sist <- round(sum(tab_distribuicao$Remanescentes))

tab_distribuicao %>% 
  select(dap, `Desbaste sistemático`,`Desbaste seletivo`,Remanescentes) %>% 
  pivot_longer(2:4, names_to = 'situacao', values_to = 'n') %>% 
  mutate(situacao = factor(situacao, levels = c('Desbaste sistemático','Desbaste seletivo','Remanescentes'), ordered = T)) %>% 
ggplot(aes(x = dap, y = n, fill = situacao))+
  geom_bar(stat = 'identity')+
  scale_fill_viridis_d()+
  scale_x_continuous(breaks = seq(0,30,5))+
  labs(x = 'Classe de DAP (cm)',
       y = 'Frequência (árvores/ha)',
       title = 'Simulação de desbaste sistemático + seletivo',
       subtitle = 'Intensidade do sitemático: 5ª linha\nIntensidade do seletivo: 1/3',
       caption = paste0('Número de árvores inicial: ', N,'\n',
                        'Número de árvores removidas no desbaste sistemático: ', n_colh_sist,'\n',
                        'Número de árvores removidas no desbaste seletivo: ', n_colh_sel,'\n',
                        'Número de árvores remanescentes: ', n_rem_sist))+
  theme_minimal()+
  theme(
    plot.title.position = 'plot',
    legend.position = 'bottom',
    legend.title = element_blank()
    )

Se quiséssemos aumentar o nível de detalhe desta modelagem, poderíamos ainda considerar que parte das árvores que serão submetidas a desbaste seletivo serão cortadas por serem defeituosas, e não por serem a menor dentre três em sequência. Nesse caso podemos calcular/estimar o percentual de árvores defeituosas do povoamento e adotar procedimento similar ao do desbaste sistemático, se considerarmos que todas as classes tem igual chance de apresentar representantes com fuste defeituoso. Não entraremos nesse nível de complexidade neste exemplo.

Vamos por fim representar graficamente todas as premissas e os resultados da nossa simulação.

dap_medio_desb <- tab_distribuicao %>% 
  mutate(dap_x_n = dap * (`Desbaste seletivo` + `Desbaste sistemático`)) %>% 
  summarise(dapmedio = sum(dap_x_n)/sum((`Desbaste seletivo` + `Desbaste sistemático`))) %>% 
  pull(dapmedio)

dap_medio_pos_desb <- tab_distribuicao %>% 
  mutate(dap_x_n = dap * Remanescentes) %>% 
  summarise(dapmedio = sum(dap_x_n)/sum(Remanescentes)) %>% 
  pull(dapmedio)

dist_tab <- tab_distribuicao %>% 
  select(dap, `Desbaste sistemático`,`Desbaste seletivo`,Remanescentes) %>% 
  pivot_longer(2:4, names_to = 'situacao', values_to = 'n') %>% 
  mutate(situacao = factor(situacao, levels = c('Desbaste sistemático','Desbaste seletivo','Remanescentes'), ordered = T))

ggplot()+
  geom_bar(aes(x = dap, y = n, fill = situacao), stat = 'identity', dist_tab)+
  geom_vline(aes(xintercept = dap, linetype = 'DAP médio pré-desbaste'), size = 1)+
  geom_vline(aes(xintercept = dap_medio_pos_desb, linetype = 'DAP médio remanescentes'), size = 1)+
  geom_vline(aes(xintercept = dap_medio_desb, linetype = 'DAP médio desbastadas'), size = 1)+
  geom_label(aes(x = dap, y = 250, label = round(dap,1)), size = 3, vjust = 1)+
  geom_label(aes(x = dap_medio_pos_desb, y = 250, label = round(dap_medio_pos_desb,1)), size = 3, vjust = 1)+
  geom_label(aes(x = dap_medio_desb, y = 250, label = round(dap_medio_desb,1)), size = 3, vjust = 1)+
  scale_fill_viridis_d()+
  scale_linetype_manual(values = c('solid','dotted','dashed'))+
  scale_x_continuous(limits = c(7.5, 20.5), breaks = seq(0,30,1))+
  scale_y_continuous(limits = c(0, 250))+
  labs(x = 'Classe de DAP (cm)',
       y = 'Frequência (árvores/ha)',
       title = 'Simulação de desbaste sistemático + seletivo',
       subtitle = 'Intensidade do sitemático: 5ª linha\nIntensidade do seletivo: 1/3',
       caption = paste0('Número de árvores inicial: ', N,'\n',
                        'Número de árvores removidas no desbaste sistemático: ', n_colh_sist,'\n',
                        'Número de árvores removidas no desbaste seletivo: ', n_colh_sel,'\n',
                        'Número de árvores remanescentes: ', n_rem_sist))+
  theme_minimal()+
  theme(
    plot.title.position = 'plot',
    legend.position = 'bottom',
    legend.box = 'vertical',
    legend.title = element_blank()
    )

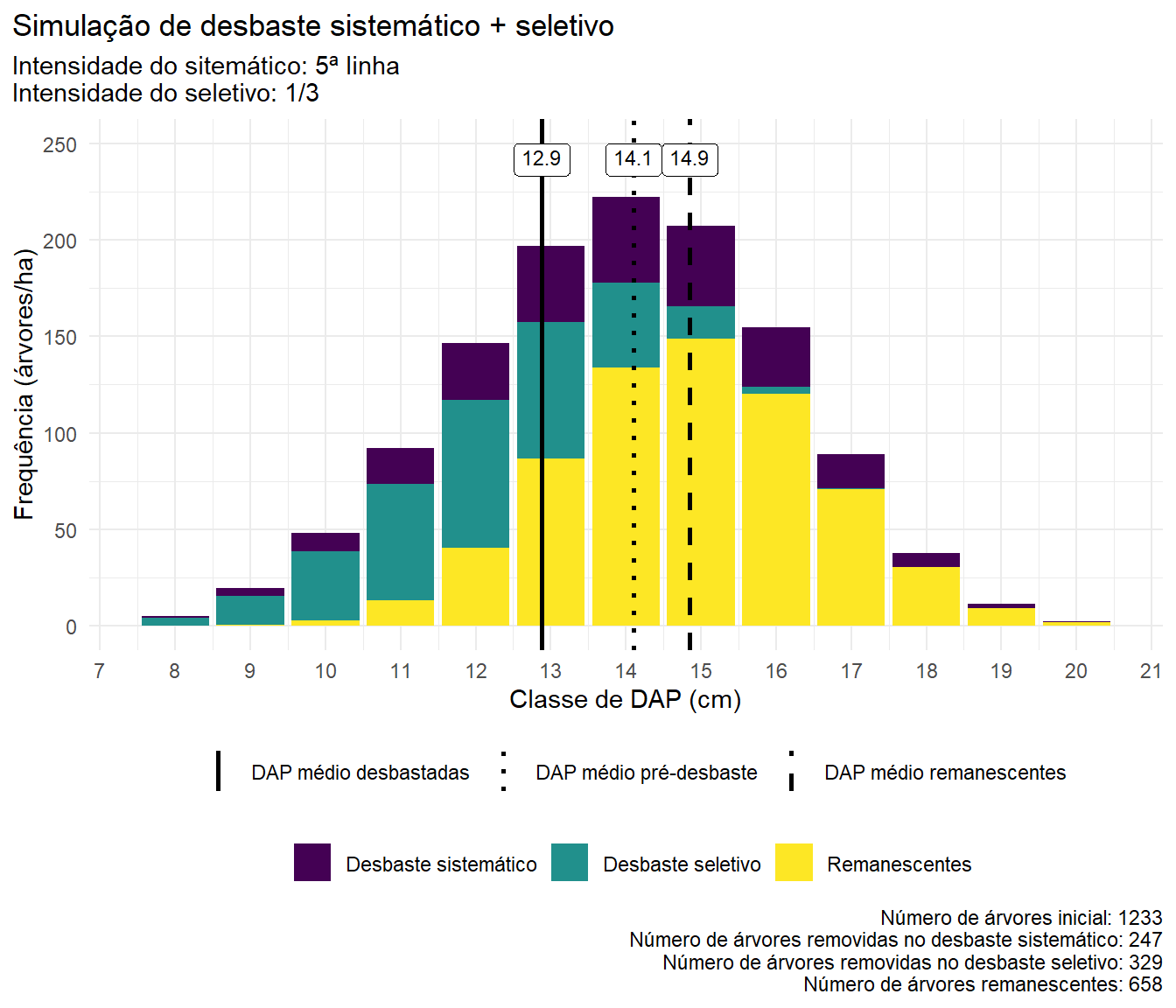
Como já mencionado, os procedimentos apresentados nesta postagem são apenas um componente para a construção de um sistema de simulação de crescimento e produção por classes diamétricas capaz de simular desbastes. A partir de tabelas de distribuição diamétrica podemos aplicar funções hipsométricas e, na sequência, funções de afilamento para obtenção de volumes totais e comerciais. Tabelas de distribuição diamétrica podem ser construídas para qualquer idade de um povoamento, desde que tenhamos dados suficientes para modelagem de variáveis como o DAP médio, DAP mínimo, área basal, entre outros, e assim calcularmos a produção esperada para diferentes idades.

Biometria
Avatar
Sérgio Costa
MSc. Engenheiro Florestal

Mestre em Engenharia Florestal pela Universidade Federal do Paraná, atualmente trabalha como Especialista em Modelagem de Dados na Arauco Forest Brasil.

comments powered by Disqus
Anterior

Relacionados