Cálculo de volumes a partir de funções de afilamento com o pacote timbeR
Introdução ao pacote timbeR
O manejo florestal voltado à obtenção de múltiplos produtos é praticado por empresas florestais que fornecem variados sortimentos de madeira com o objetivo de atender a diferentes mercados, como o de serrarias, celulose, painéis de madeira, energia, etc.
Para estas empresas, no âmbito do inventário florestal, há a necessidade de se estimar a produção de cada sortimento de madeira, visando gerar as informações necessárias para o planejamento da produção e do orçamento.
A estimativa do volume de toras de diferentes dimensões ao longo do fuste das árvores é realizado pela integração de funções de afilamento ajustadas a partir de dados de cubagem das árvores. Para aplicar esse procedimento de maneira escalável, são necessários conhecimentos estatísticos, matemáticos e, muitas vezes, de programação, e por esta razão, é comum que o processamento desses dados seja realizado por softwares comerciais específicos.
Eu particularmente não conheci, até a data deste post, um pacote do R que pudesse facilitar o processamento de inventários florestais com funções de afilamento e múltiplos produtos, e por esta razão comecei a desenvolver o timbeR.
O objetivo do pacote é fornecer funções que facilitem o ajuste e a aplicação de funções de afilamento em inventários florestais, permitindo o uso de modelos de forma variável - Bi (2000) e Kozak (2004) - como alternativas às funções tradicionais de forma fixa (polinômio do 5º grau, polinômio de potencias fracionárias e inteiras, etc.).
Podemos instalar o pacote a partir da última versão disponível no CRAN (função install_packages do R base) ou pela versão mais atual em desenvolvimento (função install_github do pacote devtools).
options(download.file.method = 'libcurl')
##################################
# Última versão disponível no CRAN
##################################
install.packages('timbeR')
#########################
# Versão do desenvolvedor
#########################
#install.packages('devtools')
devtools::install_github('sergiocostafh/timbeR')O pacote permite a utilização de três funções de afilamento:
Polinômio do 5º grau (Schöepfer, 1966)
Função de forma variável de Kozak (2004)
Função trigonométrica de forma variável de Bi (2000)
em que:
i do fuste;
i do fuste;
Para conhecermos as funções do pacote, faremos uma análise de regressão utilizando a base de dados tree_scaling que pode ser acessada quando importamos o pacote timbeR.
library(dplyr)
library(timbeR)
glimpse(tree_scaling)## Rows: 136
## Columns: 5
## $ tree_id <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2,…
## $ dbh <dbl> 14.96, 14.96, 14.96, 14.96, 14.96, 14.96, 14.96, 14.96, 14.96,…
## $ h <dbl> 15.61, 15.61, 15.61, 15.61, 15.61, 15.61, 15.61, 15.61, 15.61,…
## $ hi <dbl> 0.1561, 0.3122, 0.4683, 0.6244, 0.7805, 1.3000, 1.5610, 2.3415…
## $ di <dbl> 16.55, 15.92, 15.60, 15.18, 14.96, 14.00, 12.73, 12.10, 10.19,…A base de dados contém cinco colunas, que se referem ao id único da árvore (tree_id),
DAP (dbh), altura total (h), altura na seção i (hi) e o diâmetro na seção i (di).
Podemos ter uma ideia do perfil das árvores cubadas por meio da relação entre os diâmetros relativos e as alturas relativas (di / dbh vs hi / h).
library(ggplot2)
tree_scaling <- tree_scaling %>%
mutate(did = di/dbh,
hih = hi/h)
ggplot(tree_scaling, aes(x = hih, y = did, group = tree_id))+
geom_point()+
labs(x = 'hi/h',
y = 'di/dbh')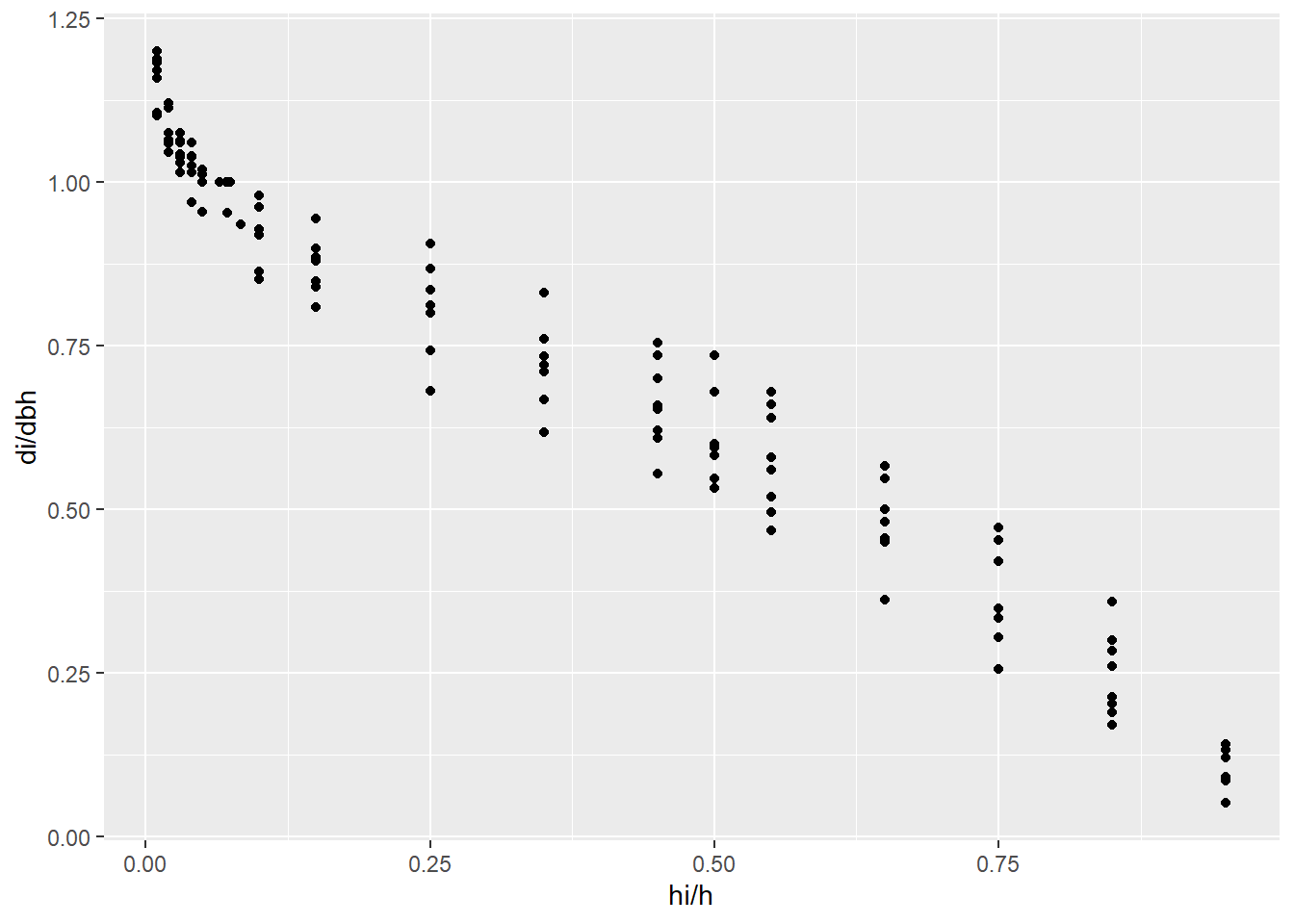
Ajuste de funções de afilamento
Agora que conhecemos a base dados, vamos iniciar a análise de regressão com o polinômio do 5º grau.
poli5 <- lm(did~hih+I(hih^2)+I(hih^3)+I(hih^4)+I(hih^5),tree_scaling)
summary(poli5)##
## Call:
## lm(formula = did ~ hih + I(hih^2) + I(hih^3) + I(hih^4) + I(hih^5),
## data = tree_scaling)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.124049 -0.029700 -0.003642 0.032621 0.112321
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.15657 0.01615 71.596 < 2e-16 ***
## hih -3.37185 0.46898 -7.190 4.55e-11 ***
## I(hih^2) 13.57792 3.40969 3.982 0.000113 ***
## I(hih^3) -29.92092 9.59285 -3.119 0.002235 **
## I(hih^4) 29.39935 11.38070 2.583 0.010893 *
## I(hih^5) -10.85327 4.78706 -2.267 0.025028 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.05469 on 130 degrees of freedom
## Multiple R-squared: 0.9697, Adjusted R-squared: 0.9685
## F-statistic: 830.8 on 5 and 130 DF, p-value: < 2.2e-16tree_scaling <- tree_scaling %>%
mutate(di_poli = predict(poli5)*dbh)
poli_rmse <- tree_scaling %>%
summarise(RMSE = sqrt(sum((di_poli-di)^2)/mean(di_poli))) %>%
pull(RMSE) %>%
round(2)
ggplot(tree_scaling, aes(x=hih))+
geom_point(aes(y = (di_poli-di)/di_poli*100))+
geom_hline(aes(yintercept = 0))+
scale_y_continuous(limits=c(-100,100), breaks = seq(-100,100,20))+
scale_x_continuous(limits=c(0,1))+
labs(x = 'hi / h', y = 'Resíduos (%)',
title = 'Polinômio do 5º grau (Schöepfer, 1966)',
subtitle = 'Dispersão dos resíduos ao longo do fuste',
caption = paste0('RMSE = ', poli_rmse,'%'))+
theme(plot.title.position = 'plot')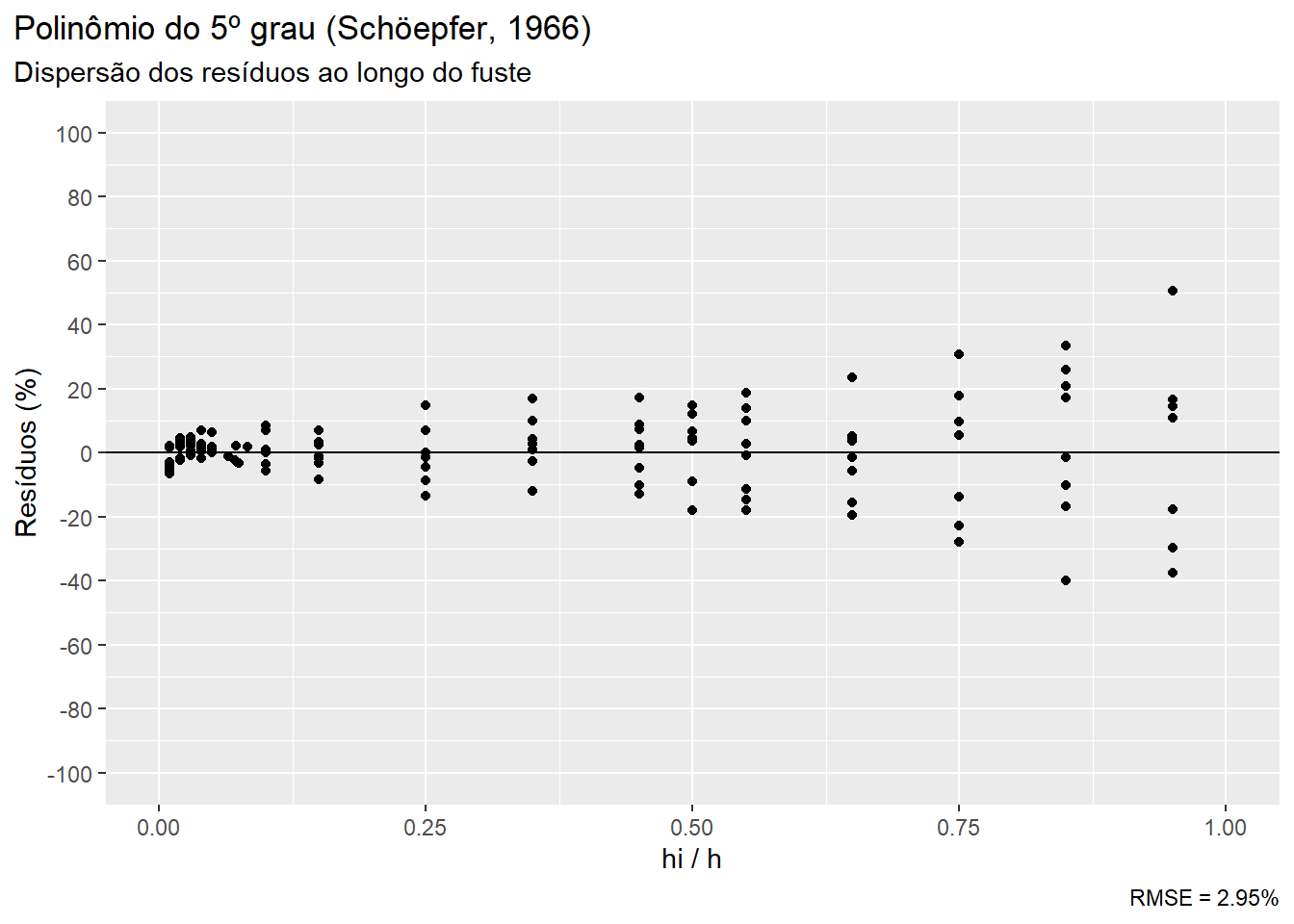
O polinômio do 5º grau é utilizado como uma função de afilamento de forma fixa, representando neste exemplo a forma média dos perfis das árvores presentes na base de dados. O ajuste resultou em um RMSE em torno de 3% e podemos notar que a variância dos resíduos é maior nas porções superiores da árvore (ponteira).
Vamos ver se o modelo de Bi (2000) pode nos trazer melhores resultados. Devido a sua natureza não linear, usaremos a função nlsLM do pacote minpack.lm para ajustar os parâmetros do modelo cuja fórmula está implementada na função taper_bi.
library(minpack.lm)
bi <- nlsLM(di ~ taper_bi(dbh, h, hih, b0, b1, b2, b3, b4, b5, b6),
data=tree_scaling,
start=list(b0=1.8,b1=-0.2,b2=-0.04,b3=-0.9,b4=-0.0006,b5=0.07,b6=-.14))
summary(bi)##
## Formula: di ~ taper_bi(dbh, h, hih, b0, b1, b2, b3, b4, b5, b6)
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## b0 1.821275 0.455063 4.002 0.000105 ***
## b1 1.417831 0.287019 4.940 2.38e-06 ***
## b2 0.142028 0.035637 3.985 0.000112 ***
## b3 -1.082588 0.301635 -3.589 0.000470 ***
## b4 -0.004008 0.003088 -1.298 0.196525
## b5 0.325254 0.053354 6.096 1.17e-08 ***
## b6 -0.735532 0.106476 -6.908 2.02e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8063 on 129 degrees of freedom
##
## Number of iterations to convergence: 5
## Achieved convergence tolerance: 1.49e-08tree_scaling <- tree_scaling %>%
mutate(di_bi = predict(bi))
bi_rmse <- tree_scaling %>%
summarise(RMSE = sqrt(sum((di_bi-di)^2)/mean(di_bi))) %>%
pull(RMSE) %>%
round(2)
ggplot(tree_scaling,aes(x=hih))+
geom_point(aes(y = (di_bi-di)/di_bi*100))+
geom_hline(aes(yintercept = 0))+
scale_y_continuous(limits=c(-100,100), breaks = seq(-100,100,20))+
scale_x_continuous(limits=c(0,1))+
labs(x = 'hi / h', y = 'Resíduos (%)',
title = 'Função trigonométrica de forma variável de Bi (2000)',
subtitle = 'Dispersão dos resíduos ao longo do fuste',
caption = paste0('RMSE = ', bi_rmse,'%'))+
theme(plot.title.position = 'plot')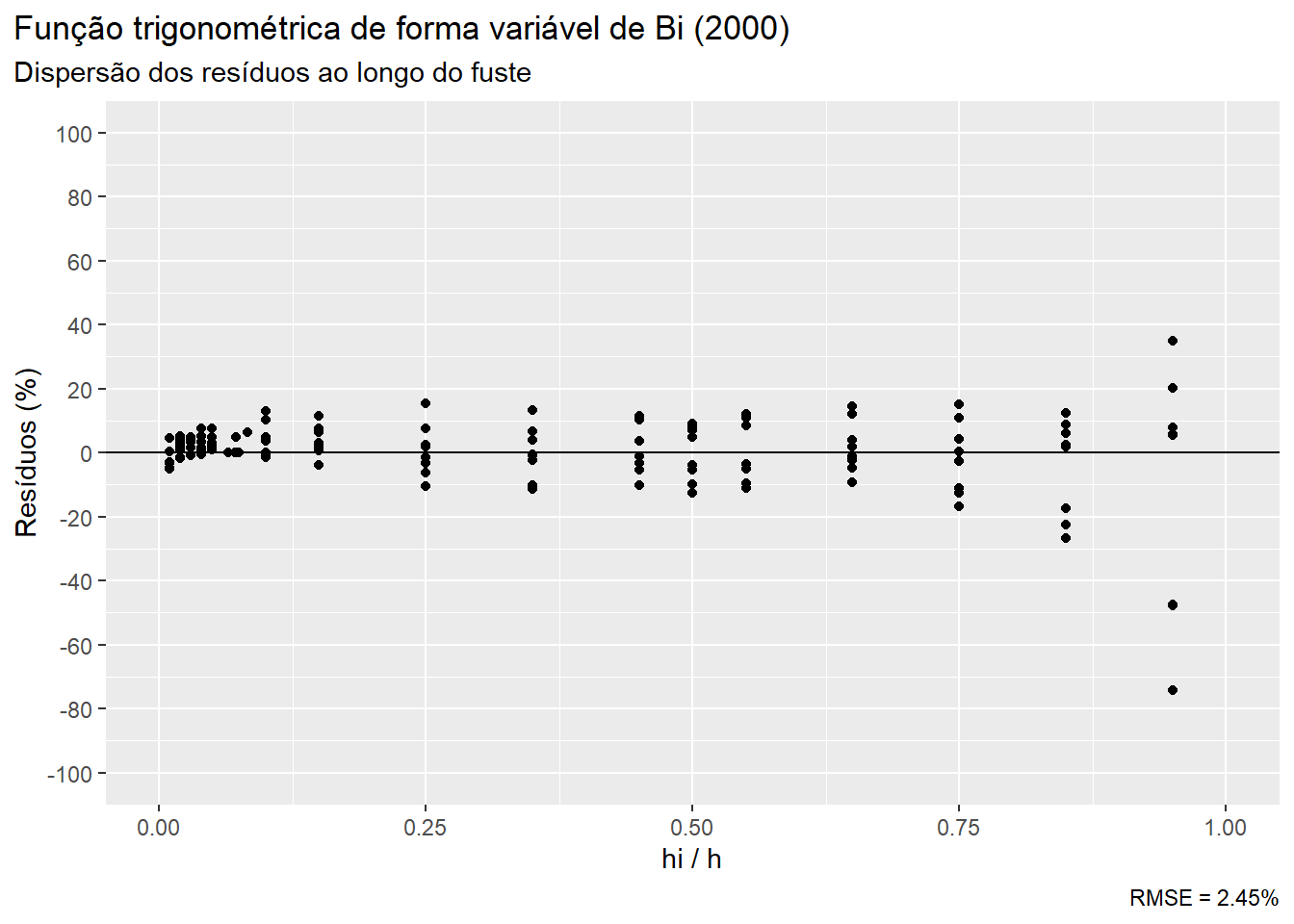
O modelo de Bi (2000) obteve melhor desempenho que a função polinomial, se tomarmos por base o RMSE. No entanto, o elevada variância das estimativas de diâmetros próximos ao topo da árvore ainda persiste. Vamos ver o que ocorre quando ajustamos o modelo de Kozak (2004) cuja fórmula está implementada na função taper_kozak. Trataremos o parâmetro p como mais um a ser estimado pela função nlsLM.
kozak <- nlsLM(di ~ taper_kozak(dbh, h, hih, b0, b1, b2, b3, b4, b5, b6, b7, b8, p),
start=list(b0=1.00,b1=.97,b2=.03,b3=.49,b4=-
0.87,b5=0.50,b6=3.88,b7=0.03,b8=-0.19, p=.1),
data = tree_scaling,
control = nls.lm.control(maxiter = 1000, maxfev = 2000)
)
summary(kozak)##
## Formula: di ~ taper_kozak(dbh, h, hih, b0, b1, b2, b3, b4, b5, b6, b7,
## b8, p)
##
## Parameters:
## Estimate Std. Error t value Pr(>|t|)
## b0 1.057e+00 5.338e-01 1.981 0.0498 *
## b1 1.088e+00 8.074e-02 13.471 < 2e-16 ***
## b2 1.120e-01 2.205e-01 0.508 0.6125
## b3 3.404e-01 5.610e-02 6.067 1.41e-08 ***
## b4 -2.823e+00 4.948e-01 -5.706 7.83e-08 ***
## b5 9.832e-01 1.192e-01 8.251 1.79e-13 ***
## b6 1.197e+01 2.902e+00 4.123 6.73e-05 ***
## b7 1.082e-01 4.673e-02 2.316 0.0222 *
## b8 -4.930e-01 2.951e-01 -1.671 0.0972 .
## p 2.149e-18 6.523e-13 0.000 1.0000
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.6276 on 126 degrees of freedom
##
## Number of iterations to convergence: 100
## Achieved convergence tolerance: 1.49e-08tree_scaling <- tree_scaling %>%
mutate(di_kozak = predict(kozak))
kozak_rmse <- tree_scaling %>%
summarise(RMSE = sqrt(sum((di_kozak-di)^2)/mean(di_kozak))) %>%
pull(RMSE) %>%
round(2)
ggplot(tree_scaling, aes(x=hih))+
geom_point(aes(y = (di_kozak-di)/di_kozak*100))+
geom_hline(aes(yintercept = 0))+
scale_y_continuous(limits=c(-100,100), breaks = seq(-100,100,20))+
scale_x_continuous(limits=c(0,1))+
labs(x = 'hi / h', y = 'Resíduos (%)',
title = 'Função de forma variável de Kozak (2004)',
subtitle = 'Dispersão de resíduos ao longo do fuste',
caption = paste0('RMSE = ', kozak_rmse,'%'))+
theme(plot.title.position = 'plot')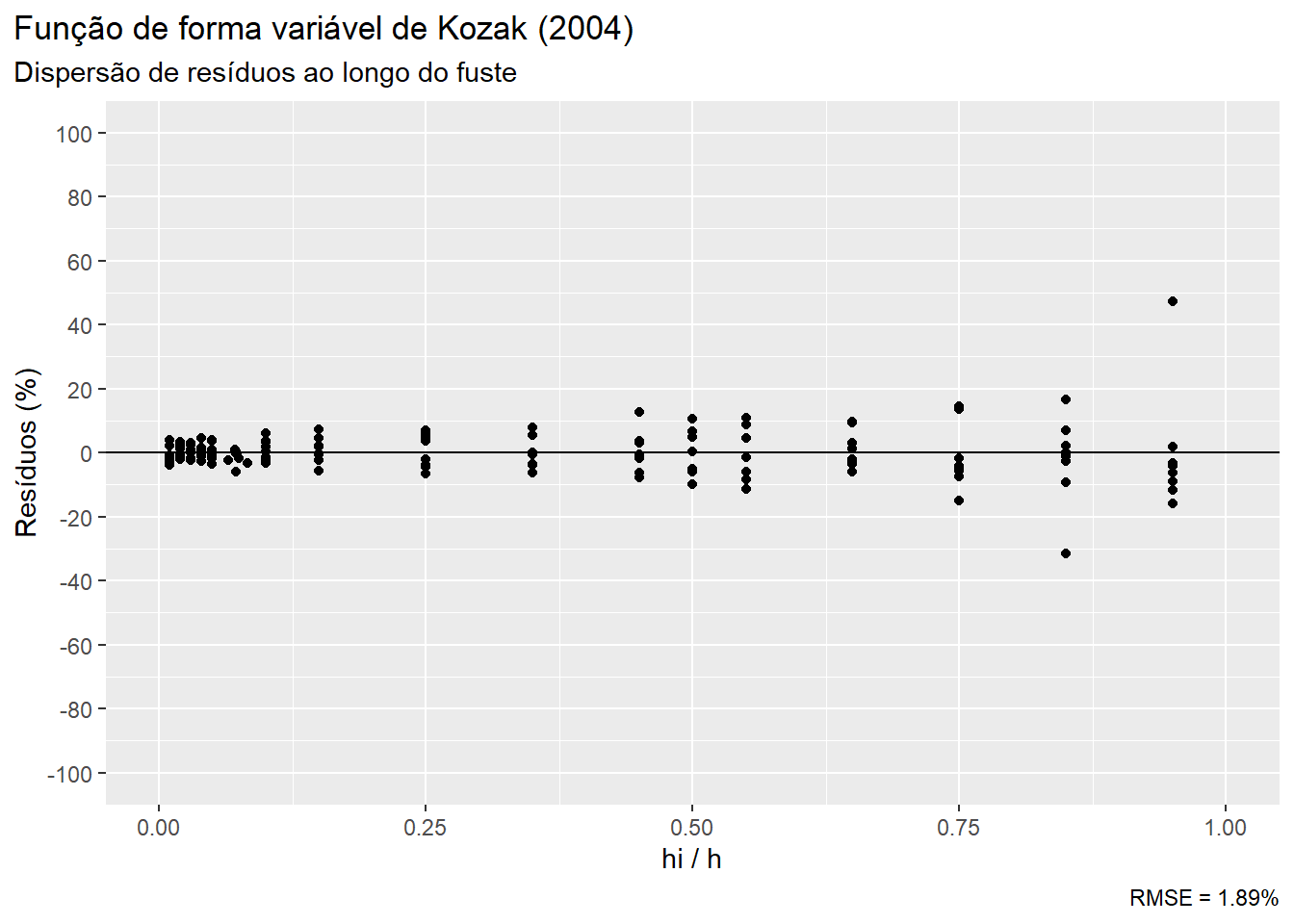 No ajuste do modelo de Kozak (2004) foi possível obter um RMSE abaixo de 2% e ainda minimizar a dispersão dos resíduos das estimativas de diâmetro na porção superior das árvores. Para a base de dados apresentada, este foi o modelo de melhor desempenho.
No ajuste do modelo de Kozak (2004) foi possível obter um RMSE abaixo de 2% e ainda minimizar a dispersão dos resíduos das estimativas de diâmetro na porção superior das árvores. Para a base de dados apresentada, este foi o modelo de melhor desempenho.
Aplicando as equações ajustadas
Agora iremos explorar as funções presentes no pacote timbeR que permitem aplicar os modelos ajustados na prática. A tabela a seguir apresenta a funções auxiliares de cada modelo, agrupadas por uso.
| Uso | Polinômio do 5° grau | Bi (2002) | Kozak (2004) |
|---|---|---|---|
| Estimar o diâmetro a uma altura definida | poly5_di |
bi_di |
kozak_di |
| Estimar a altura em que determinado diâmetro ocorre | poly5_hi |
bi_hi |
kozak_hi |
| Estimar o volume total ou parcial do fuste | poly5_vol |
bi_vol |
kozak_vol |
| Estimar o volume e a quantidade de toras por sortimento | poly5_logs |
bi_logs |
kozak_logs |
| Visualizar a simulação do traçamento das toras no fuste | poly5_logs_plot |
bi_logs_plot |
kozak_logs_plot |
Agora iremos aplicar as funções descritas na tabela usando os modelos ajustados na seção anterior. Para facilitar a compreensão, vamos começar aplicando as funções a uma única árvore. Iniciamos pela definição das medidas de altura total e DAP.
dbh <- 25
h <- 20Todas as funções auxiliares possuem o argumento coef, em que um vetor de coeficientes do modelo deve ser declarado. Este objeto pode ser criado pelo uso da função coef, da coleção base do R. Para o modelo de Kozak (2004) é necessário declarar o parâmetro p separadamente.
coef_poli <- coef(poli5)
coef_bi <- coef(bi)
coef_kozak <- coef(kozak)[-10]
p_kozak <- coef(kozak)[10]Vamos estimar o diâmetro (di) a uma dada altura (hi). Assumimos que hi = 15 para este exemplo.
hi <- 15
poly5_di(dbh, h, hi, coef_poli)## [1] 9.224517bi_di(dbh, h, hi, coef_bi)## [1] 8.559173kozak_di(dbh, h, hi, coef_kozak, p = p_kozak)## [1] 8.92263Nota-se que há certa variação entre as predições dos modelos ajustados. Podemos observar melhor esse efeito representando o perfil completo da árvore que estamos usando como exemplo.
hi <- seq(0.1,h,.1)
ggplot(mapping=aes(x=hi))+
geom_line(aes(y=poly5_di(dbh, h, hi, coef_poli), linetype = 'Polinômio do 5º grau'))+
geom_line(aes(y=bi_di(dbh, h, hi, coef_bi), linetype = 'Bi (2000)'))+
geom_line(aes(y=kozak_di(dbh, h, hi, coef_kozak, p_kozak), linetype = 'Kozak (2004)'))+
scale_linetype_manual(name = 'Modelos ajustados', values = c('solid','dashed','dotted'))+
labs(x = 'hi (m)',
y = 'di estimado (cm)')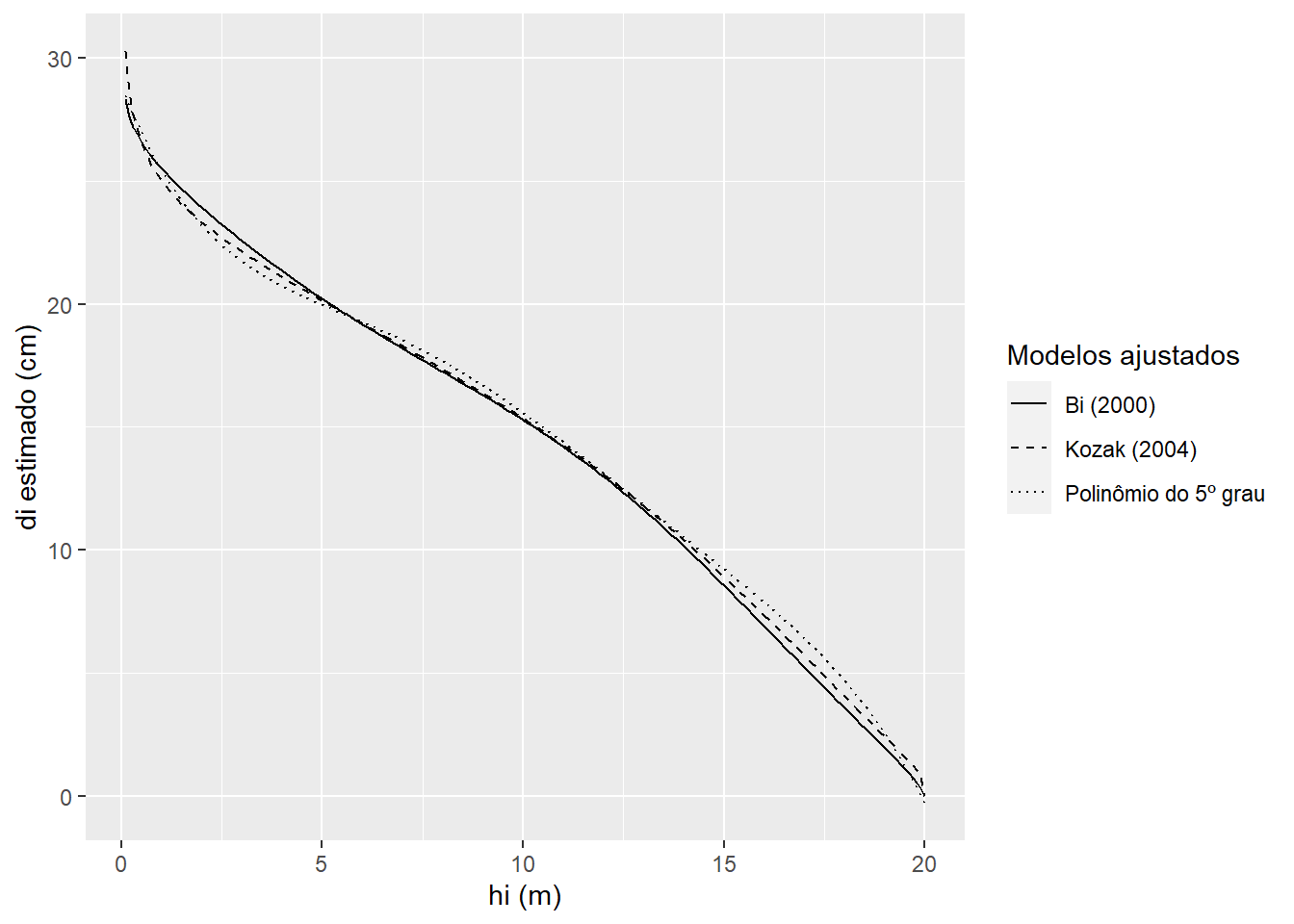
Para predição da altura em que determinado diâmetro ocorre, o procedimento é similar ao apresentado acima, mas desta vez devemos declarar o argumento di em vez de hi, para as funções correspondentes.
di <- 10
poly5_hi(dbh, h, di, coef_poli)## [1] 14.40821bi_hi(dbh, h, di, coef_bi)## [1] 14.09805kozak_hi(dbh, h, di, coef_kozak, p_kozak)## [1] 14.2817Neste caso, a aplicação dos diferentes modelos resultou em predições bastante similares.
As funções para estimativa de volumes total e parcial são similares às apresentadas até aqui, com alguns argumentos adicionais. Os procedimentos a seguir calculam o volume do fuste completo.
poly5_vol(dbh, h, coef_poli)## [1] 0.414718bi_vol(dbh, h, coef_bi)## [1] 0.4128356kozak_vol(dbh, h, coef_kozak, p_kozak)## [1] 0.413102O volume parcial também pode ser estimado ao declarar a altura inicial h0 e a altura final hi.
hi = 15
h0 = .2
poly5_vol(dbh, h, coef_poli, hi, h0)## [1] 0.3884416bi_vol(dbh, h, coef_bi, hi, h0)## [1] 0.3901346kozak_vol(dbh, h, coef_kozak, p_kozak, hi, h0)## [1] 0.3863585Finalmente, vamos ver como os modelos estimam o volume e a quantidade de toras para diferentes produtos da madeira. Para isso, precisamos definir os sortimentos.
A tabela de sortimentos deve conter cinco colunas, que podem ter qualquer nome, mas devem estar na seguinte ordem: diâmetro da tora na ponta fina, em centímetros; comprimento mínimo da tora (líquido), em metros; comprimento máximo da tora (líquido), em metros; e a perda resultante do traçamento de cada tora, em centímetros. Um ponto de atenção é que as linhas da tabela representam os produtos da madeira, e estes devem estar ordenados do mais valioso para o menos valioso, de modo que o algoritmo de extração de toras priorize aos produtos de maior valor comercial.
Em nosso exemplo, utilizaremos a seguinte tabela de produtos:
| Name | SED | MINLENGTH | MAXLENGTH | LOSS |
|---|---|---|---|---|
| > 15 | 15 | 2.65 | 2.65 | 5 |
| 4-15 | 4 | 2 | 4.2 | 5 |
assortments <- data.frame(
NAME = c('> 15','4-15'),
SED = c(15,4),
MINLENGTH = c(2.65,2),
MAXLENGTH = c(2.65,4.2),
LOSS = c(5,5)
)Agora podemos estimar o volume e a quantidade de toras ao longo do fuste de nossa árvore exemplo.
poly5_logs(dbh, h, coef_poli, assortments)## $volumes
## # A tibble: 1 × 2
## `> 15` `4-15`
## <dbl> <dbl>
## 1 0.293 0.111
##
## $logs
## # A tibble: 1 × 2
## `> 15` `4-15`
## <dbl> <dbl>
## 1 3 2bi_logs(dbh, h, coef_bi, assortments)## $volumes
## # A tibble: 1 × 2
## `> 15` `4-15`
## <dbl> <dbl>
## 1 0.299 0.107
##
## $logs
## # A tibble: 1 × 2
## `> 15` `4-15`
## <dbl> <dbl>
## 1 3 2kozak_logs(dbh, h, coef_kozak, p_kozak, assortments)## $volumes
## # A tibble: 1 × 2
## `> 15` `4-15`
## <dbl> <dbl>
## 1 0.296 0.109
##
## $logs
## # A tibble: 1 × 2
## `> 15` `4-15`
## <dbl> <dbl>
## 1 3 2Há diversos argumentos adicionais nas funções que estimam volume/quantidades de toras que alteram a maneira como os cálculos são realizados. É possível, por exemplo, realizar downgrades nas toras de árvores defeituosas a partir da altura em que o dano ocorre, calcular o volume de fustes quebrados de maneira adequada e usar diferentes alturas de toco para árvores bifurcadas desde a base. Recomendo a leitura da documentação dessas funções para melhor compreender suas funcionalidades.
Para finalizarmos a demonstração de funções, vamos ver como o pacote timbeR permite visualizar como o traçamento das toras ao longo do fuste de uma árvore ocorre nas funções de estimativa de volume/quantidade de toras. Os argumentos para estas funções, são praticamente os mesmos das funções anteriormente apresentadas.
poly5_logs_plot(dbh, h, coef_poli, assortments, stump_height = 0.2, lang = 'pt-BR')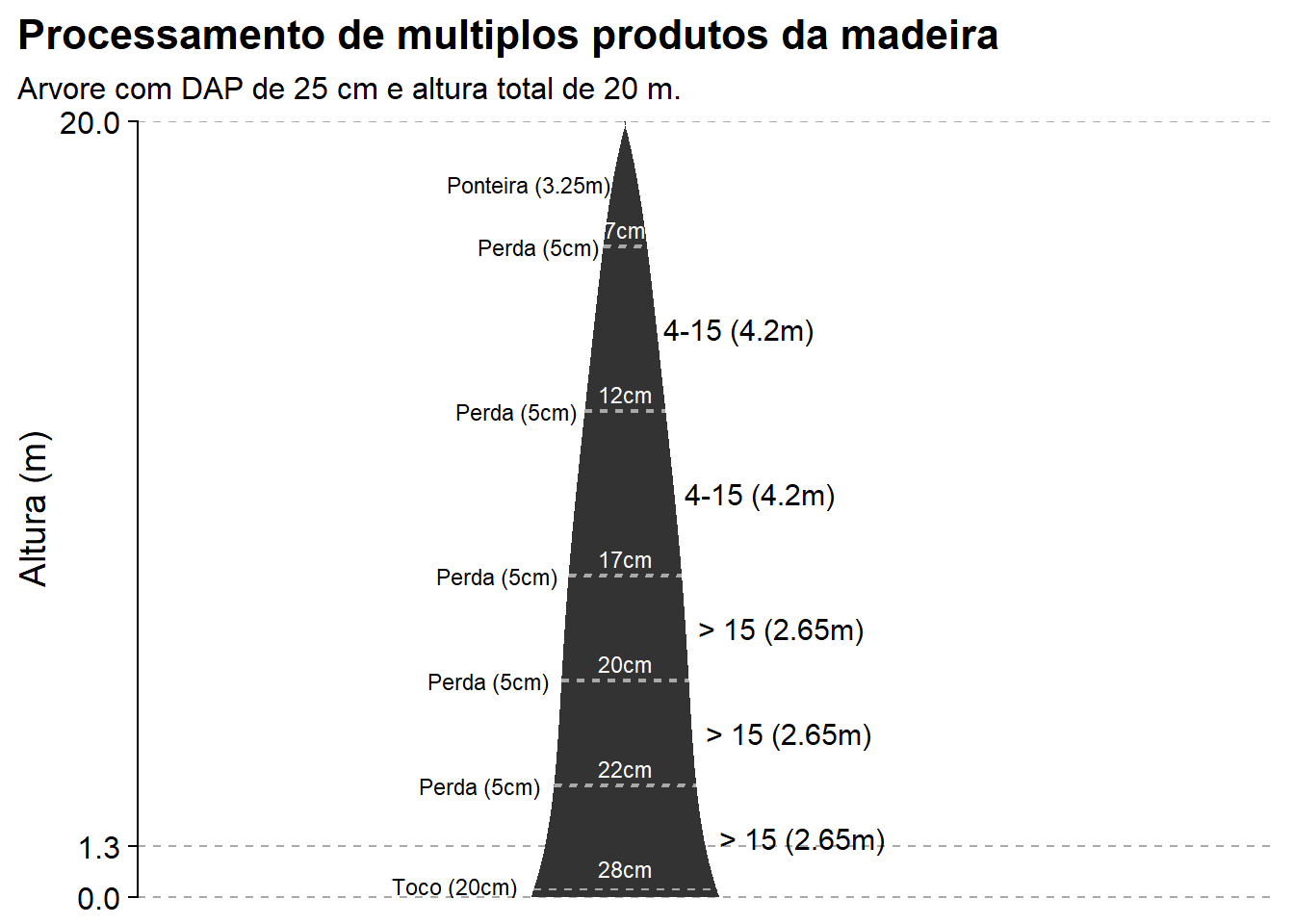
bi_logs_plot(dbh, h, coef_bi, assortments, stump_height = 0.2, lang = 'pt-BR')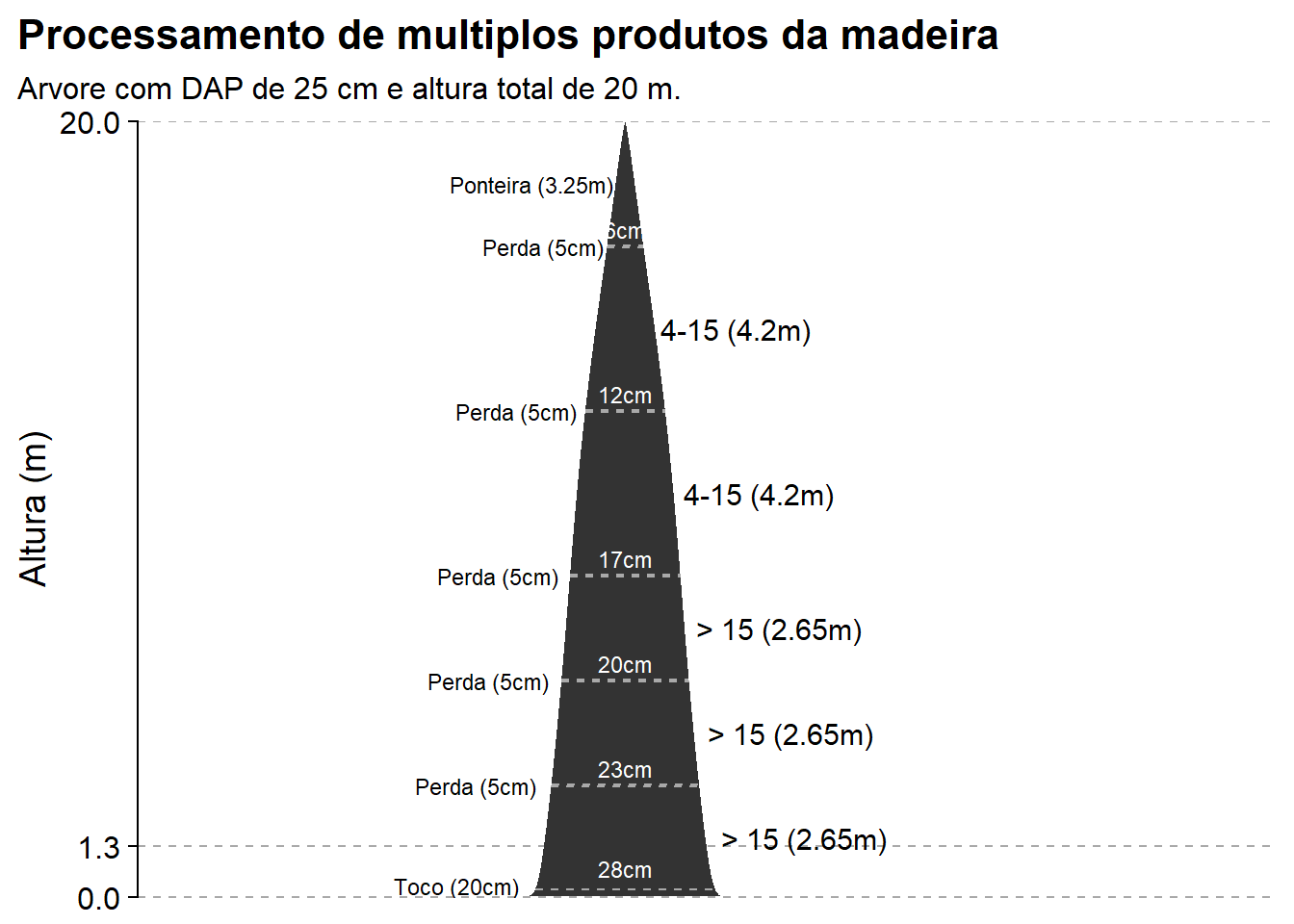
kozak_logs_plot(dbh, h, coef_kozak, p_kozak, assortments, stump_height = 0.2, lang = 'pt-BR')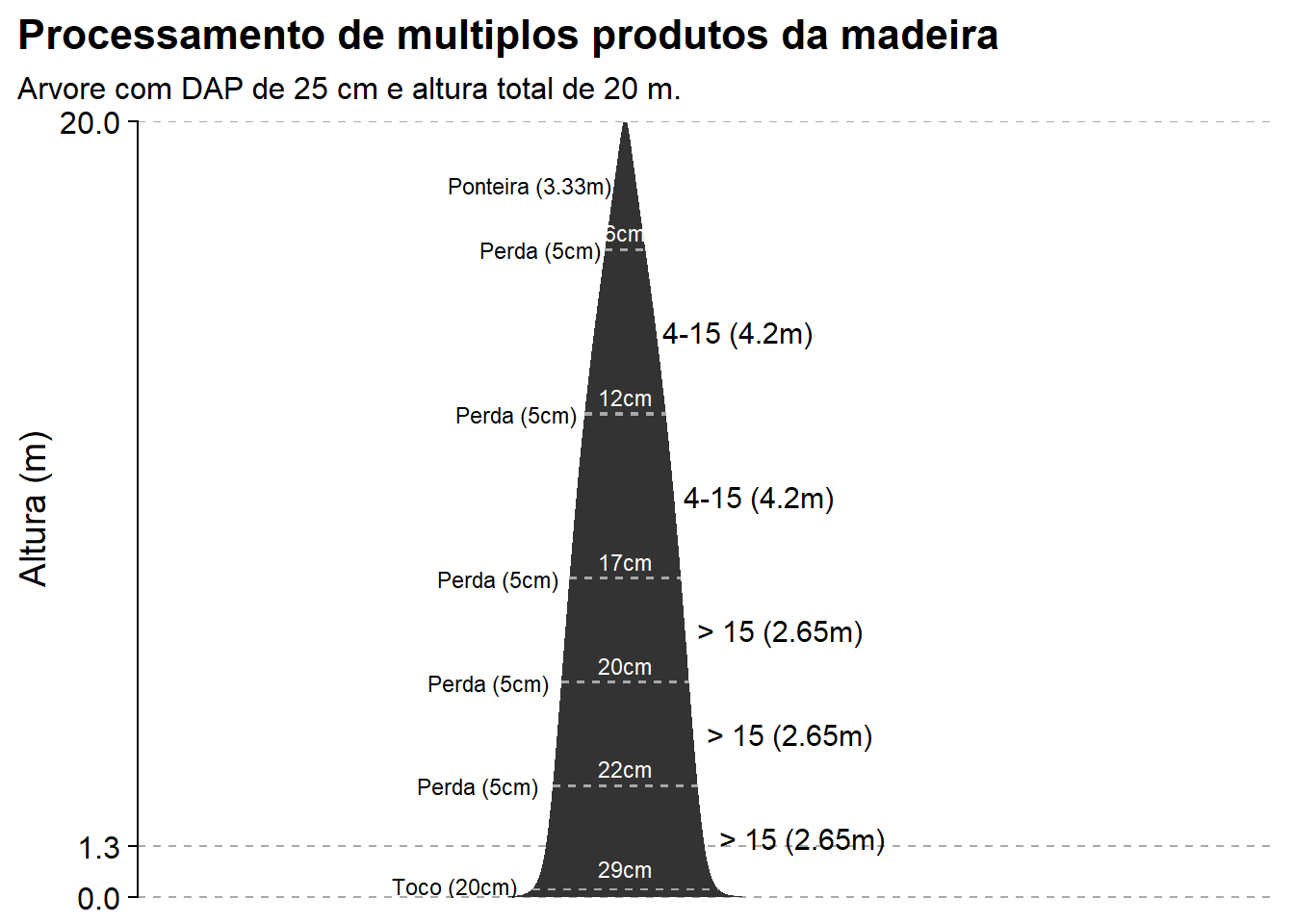
Usando as funções do pacote timbeR em escala de inventário florestal
As funções para estimativa de volume/quantidade de toras são executadas uma árvore por vez. A aplicação dessas funções a múltiplas árvores pode ser realizada de diferentes maneiras. Seguem alguns exemplos dessa aplicação utilizando a função base do R mapply e utilizando a função pmap do pacote purrr.
# Usando mapply
tree_data <- data.frame(dbh = c(18.3, 23.7, 27.2, 24.5, 20, 19.7),
h = c(18, 24, 28, 24, 18.5, 19.2))
assortment_vol <- mapply(
poly5_logs,
dbh = tree_data$dbh,
h = tree_data$h,
SIMPLIFY = T,
MoreArgs = list(
coef = coef_poli,
assortments = assortments,
stump_height = 0.2,
total_volume = T,
only_vol = T
)
) %>%
t()
assortment_vol## > 15 4-15 Total
## [1,] 0.06525096 0.124656 0.1999943
## [2,] 0.3303831 0.09825193 0.4472505
## [3,] 0.5307287 0.1305737 0.687288
## [4,] 0.3530639 0.1051031 0.4779542
## [5,] 0.1335897 0.09999402 0.2455131
## [6,] 0.1310012 0.1044527 0.247216# Unindo tree_data e a tabela de volumes
library(tidyr)
cbind(tree_data, assortment_vol) %>%
unnest()## # A tibble: 6 × 5
## dbh h `> 15` `4-15` Total
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 18.3 18 0.0653 0.125 0.200
## 2 23.7 24 0.330 0.0983 0.447
## 3 27.2 28 0.531 0.131 0.687
## 4 24.5 24 0.353 0.105 0.478
## 5 20 18.5 0.134 0.100 0.246
## 6 19.7 19.2 0.131 0.104 0.247# Usando pmap
library(purrr)
tree_data %>%
mutate(coef = list(coef_poli),
assortments = list(assortments),
stump_height = 0.2,
total_volume = T,
only_vol = T) %>%
mutate(assortment_vol = pmap(.,poly5_logs)) %>%
select(dbh, h, assortment_vol) %>%
unnest(assortment_vol)## # A tibble: 6 × 5
## dbh h `> 15` `4-15` Total
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 18.3 18 0.0653 0.125 0.200
## 2 23.7 24 0.330 0.0983 0.447
## 3 27.2 28 0.531 0.131 0.687
## 4 24.5 24 0.353 0.105 0.478
## 5 20 18.5 0.134 0.100 0.246
## 6 19.7 19.2 0.131 0.104 0.247Aqui chegamos ao fim da postagem. O pacote estará em constante desenvolvimento para que novas funções e funcionalidades possam ser contempladas nas próximas versões. Toda ajuda é bem vinda para melhoria e identificação de bugs. Até a próxima!
Referências
Bi, H. (2000). Trigonometric variable-form taper equations for Australian eucalypts. Forest Science, 46(3), 397-409.
Kozak, A. (2004). My last words on taper equations. The Forestry Chronicle, 80(4), 507-515.
Schöepfer, W. (1966). Automatisierung dês Massen, Sorten und Wertberechung stender Waldbestande Schriftenreihe Bad. [S.I.]: Wurtt-Forstl.